Très belle géométrie :)

par **benekire2** » 21 Oct 2009, 15:30

alors on a:

Mais ca nous mène a quoi, faut remplacer les x y z après ?

par **Timothé Lefebvre** » 21 Oct 2009, 15:31

Je dois y aller mais rapidement, ça se simplifie. Pose 1/8 facteur de ...

A toute

par **benekire2** » 21 Oct 2009, 15:32

ok, a toute!
J'ai donc

il faut donc montrer que

est supérieur a 2.

par **benekire2** » 21 Oct 2009, 17:27

et après du coup, comment je fais pour démontrer ca ?

par **Timothé Lefebvre** » 21 Oct 2009, 17:31

Tu dois faire des erreurs de calcul.

Moi j'ai

Ce qui revient à

Et enfin à

par **benekire2** » 21 Oct 2009, 17:33

ok, mais je comprends pas la première et deuxième ligne, il y a une rècle pour passer d'une égalité à une innégalité?

par **Timothé Lefebvre** » 21 Oct 2009, 17:36

On l'obtient juste par substitution.

Je crois que j'ai un autre exo qui traite de la transfo de Ravi pour une inégalité dans un triangle. Je remets la main dessus et je le poste d'ici ce soir.

par **benekire2** » 21 Oct 2009, 17:38

Je t'avoue que je suis dans le flou, comment on fait la substitution ici ?? et avec quoi ?? !j'ai du mal a comprendre.

par **benekire2** » 21 Oct 2009, 18:06

Dans ta deuxième ligne tim, c'est pas plutôt

J'arrive pas a suivre le raisonement sur la fin :mur:

par **benekire2** » 21 Oct 2009, 19:30

c'est surtout le passage , subitement à l'inégalité qui me chagrine...

par **Timothé Lefebvre** » 21 Oct 2009, 20:00

benekire2 a écrit:Dans ta deuxième ligne tim, c'est pas plutôt

J'arrive pas a suivre le raisonement sur la fin :mur:

Oui, tu as raison, j'ai fait une faute de frappe.

En y réfléchissant, on pouvait aussi s'en tirer (beaucoup plus difficilement) avec de la trigonométrie. Mais c'est assez sport.

par **benekire2** » 21 Oct 2009, 20:09

ok, alors ultime question: Comment passer de ta première à ta deuxième ligne ? C'est le seul point qu'il me faut éclaircir

par **Timothé Lefebvre** » 21 Oct 2009, 20:12

Ben l'embêtant c'est que ça me paraît parfaitement logique.
Si le rapport est égal à

alors il est forcément strictement supérieur à

.

par **benekire2** » 21 Oct 2009, 20:14

Timothé Lefebvre a écrit:Ben l'embêtant c'est que ça me paraît parfaitement logique.
Si le rapport est égal à alors il est forcément strictement supérieur à .

je suis d'accord mais, c'est un théorème, lequel ( y a bien un théorème qui doit dire ca ?? ) enfin..

par **benekire2** » 21 Oct 2009, 20:32

oula, je viens de capter mais je trouve que c'est bizarre, parce qu'on est obligé d'admettre ca sans trop le prouver...

par **Zweig** » 22 Oct 2009, 12:42

Salut,

Soit

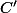
un cercle et 6 cercles

,

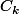
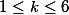
tangents intérieurement à

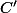
et tels que

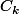
soit tangent extérieurement à

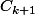
, pour tout

.
On note

,

et

leur point de tangence avec

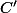
(voir figure).

Montrer que les droites

,

et

sont concourantes.

Très belle géométrie :)

Qui est en ligne