bonjour je suis en 2nd et j ai un dm de maths
I) Sur un pentagone (ABCDE), on définit une tourniquette : en parlant d'un point I du segment [AB] on construit la parallèle à (AC) qui coupe [BC] en J, puis de J la parallèle à (BD) qui coupe [CD] en K la parallèle à (CE) qui coupe [DE] en L, puis de L la parallèle à (AD) qui coupe [AE] en M, puis de M la parallèle à (BE) qui coupe [AB] en N et ainsi de suite.
Démontrer que la tourniquette se reforme au second tour.
pourriez vous m'aider a le faire svp
merci d'avance
Tourniquette
4 messages
- Page 1 sur 1
Re: Tourniquette
Bonjour
Tout repose sur les paralleles et les triangles isoceles
Soit AI = a
le theoreme de Thales dans ler triangle ABC montre que CJ = AI = a
de proche en proche on voit que AI=CJ=CK=LE=EM = a
soient les lettres primées pour le second tour
EM = BI'=a avec I' intersection de AB et de la parallele a EB
et BI'=BJ'=DK'=DL'=M'A= a
La parallele a EB tracée a partir de M' coupe AB en I" tel que AI" = M'A = a
donc I et I" sont confondus et on reforme la tournette......
Tout repose sur les paralleles et les triangles isoceles
Soit AI = a
le theoreme de Thales dans ler triangle ABC montre que CJ = AI = a
de proche en proche on voit que AI=CJ=CK=LE=EM = a
soient les lettres primées pour le second tour
EM = BI'=a avec I' intersection de AB et de la parallele a EB
et BI'=BJ'=DK'=DL'=M'A= a
La parallele a EB tracée a partir de M' coupe AB en I" tel que AI" = M'A = a
donc I et I" sont confondus et on reforme la tournette......
Re: Tourniquette
merci si le pentagone n'est pas régulier , la tourniquette marche quand meme mais il n'y a plus de triangle isocèle pour expliquer
merci de votre aide
merci de votre aide
Re: Tourniquette
Salut,
Perso, je ferais ça avec des vecteurs : si au départ pour un certain réel
pour un certain réel  alors
alors 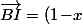\vec{BA}) donc
donc 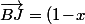\vec{BC}) donc
donc  donc
donc  , etc...
, etc...
Et lorsque tu revient pour la première fois sur la première droite (AB), deux cas se présentent :
- Le nombre de coté du polygone est pair => on retombe alors sur le point de départ.
- Le nombre de coté du polygone est impair => on retombe sur le symétrique du point de départ par rapport au milieu de [AB] donc en faisant un deuxième tour, on retombe sur le point de départ.
Perso, je ferais ça avec des vecteurs : si au départ
Et lorsque tu revient pour la première fois sur la première droite (AB), deux cas se présentent :
- Le nombre de coté du polygone est pair => on retombe alors sur le point de départ.
- Le nombre de coté du polygone est impair => on retombe sur le symétrique du point de départ par rapport au milieu de [AB] donc en faisant un deuxième tour, on retombe sur le point de départ.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
