F(x)=12
31 messages
- Page 1 sur 2 - 1, 2
F(x)=12
Bonjour,voila j'ai un exercice à faire et je bloque sur une question. voici l'exercice
Soit f la fonction définie sur par : f(x) = (3 - x)(4 + 2x).
1) Montrer que f(x) = - 2x ² + 2x + 12 puis que f(x)= 25/2-2(x-1/2)²
2) a) Résoudre l'équation f(x) = 0.
b) Etablir le tableau de signes de f.
c) En déduire les solutions de l'inéquation f(x) plus grand ou égal à 0 .
3) a) Déterminer l'intersection de la courbe représentative de f avec l'axe des ordonnées.
b) Résoudre f(x) = 12.
4) a) Dresser le tableau de variations de f.
b) Donner son extremum. En quelle valeur de x est-il atteint ?
c) Donner, dans chaque cas, un encadrement de f(x) en justifiant :
-3 ;) x ;) - 1 ;
2 ;) x ;)2,5.
je bloque à la 3)B merci de m'aider
Soit f la fonction définie sur par : f(x) = (3 - x)(4 + 2x).
1) Montrer que f(x) = - 2x ² + 2x + 12 puis que f(x)= 25/2-2(x-1/2)²
2) a) Résoudre l'équation f(x) = 0.
b) Etablir le tableau de signes de f.
c) En déduire les solutions de l'inéquation f(x) plus grand ou égal à 0 .
3) a) Déterminer l'intersection de la courbe représentative de f avec l'axe des ordonnées.
b) Résoudre f(x) = 12.
4) a) Dresser le tableau de variations de f.
b) Donner son extremum. En quelle valeur de x est-il atteint ?
c) Donner, dans chaque cas, un encadrement de f(x) en justifiant :
-3 ;) x ;) - 1 ;
2 ;) x ;)2,5.
je bloque à la 3)B merci de m'aider
Bonjour,
rappelle toi que tu as plusieurs expression de ta fonction f.
f(x) = (3 - x)(4 + 2x)
= - 2x ² + 2x + 12
= 25/2-2(x-1/2)²
L'une de ces trois expression est adaptée à résoudre f(x)=12, laquelle ?
rappelle toi que tu as plusieurs expression de ta fonction f.
f(x) = (3 - x)(4 + 2x)
= - 2x ² + 2x + 12
= 25/2-2(x-1/2)²
L'une de ces trois expression est adaptée à résoudre f(x)=12, laquelle ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
juudu62 a écrit:Bonjour,voila j'ai un exercice à faire et je bloque sur une question. voici l'exercice
Soit f la fonction définie sur par : f(x) = (3 - x)(4 + 2x).
1) Montrer que f(x) = - 2x ² + 2x + 12 puis que f(x)= 25/2-2(x-1/2)²
2) a) Résoudre l'équation f(x) = 0.
b) Etablir le tableau de signes de f.
c) En déduire les solutions de l'inéquation f(x) plus grand ou égal à 0 .
3) a) Déterminer l'intersection de la courbe représentative de f avec l'axe des ordonnées.
b) Résoudre f(x) = 12.
4) a) Dresser le tableau de variations de f.
b) Donner son extremum. En quelle valeur de x est-il atteint ?
c) Donner, dans chaque cas, un encadrement de f(x) en justifiant :
-3x
- 1 ;
2x
2,5.
je bloque à la 3)B merci de m'aider
reprends la 1° expression de f(x) les 12 s'éliminent ensuite tu mets x en facteur
Calcule la dérivée de ta fonction f (en prenant  \quad = \quad -2x^2+2x+12) ).
).
Étudie le tableau de signe de ta dérivée (dans quel intervalle est-elle négative, dans quel intervalle est-elle positive). Tu sais que f est croissante lorsque f'(x)>0 et décroissante lorsque f'(x)<0. Ca va te permettre de déduire les variations de f du tableau de signe de sa dérivée.
Si tu n'y arrives toujours pas, je ferai les premières étapes avec toi.
Étudie le tableau de signe de ta dérivée (dans quel intervalle est-elle négative, dans quel intervalle est-elle positive). Tu sais que f est croissante lorsque f'(x)>0 et décroissante lorsque f'(x)<0. Ca va te permettre de déduire les variations de f du tableau de signe de sa dérivée.
Si tu n'y arrives toujours pas, je ferai les premières étapes avec toi.
oui,j'aimerais bien qu'on le fasse ensemble parce que moi j'avais fait ça
Etape n°1 : (3 - x)*(4 + 2*x) est de la forme u * v avec u = 3 - x et v = 4 + 2*x
or (u * v)' = u' * v + u * v'
Etape n°2 : 3 - x est de la forme u - v avec u = 3 et v = x or (u - v)' = u' - v'
Etape n°3 : 4 + 2*x est de la forme u + v avec u = 4 et v = 2*x or (u + v)' = u' + v'
Etape n°4 : 2*x est de la forme ku
or (ku)' = k u' avec k = 2 et u = x
f'(x)=(0-)*(4 + 2x)+(3 - x)*(0+ 2)
mais je n'arrive pas a faire la suite et le - apres le 0 me semble bizarre donc si je dévelloppe sans cela me fait
=0*4+0*2x+3*0+3*2-x*0-x*2
=-2x+6
voila est maintenant ( si ma fonction sans le - est bonne biensur !! )
Etape n°1 : (3 - x)*(4 + 2*x) est de la forme u * v avec u = 3 - x et v = 4 + 2*x
or (u * v)' = u' * v + u * v'
Etape n°2 : 3 - x est de la forme u - v avec u = 3 et v = x or (u - v)' = u' - v'
Etape n°3 : 4 + 2*x est de la forme u + v avec u = 4 et v = 2*x or (u + v)' = u' + v'
Etape n°4 : 2*x est de la forme ku
or (ku)' = k u' avec k = 2 et u = x
f'(x)=(0-)*(4 + 2x)+(3 - x)*(0+ 2)
mais je n'arrive pas a faire la suite et le - apres le 0 me semble bizarre donc si je dévelloppe sans cela me fait
=0*4+0*2x+3*0+3*2-x*0-x*2
=-2x+6
voila est maintenant ( si ma fonction sans le - est bonne biensur !! )
Il y a de bonnes idées mais tu décompose trop et donc tu te perds.
ça c'est très bien.
Maintenant tu dois écrire directement (ça doit être dans ton cours, ou tu le fais de tête) :
u(x) = -x+3 => u' (x) = -1
v(x) = 2x+4 => v' (x) = 2
donc (uv)' = ...
Maintenant pour calculer une dérivée il vaut mieux utiliser la forme dévelppée (comme suggéré précédemment).
(3 - x)*(4 + 2*x) est de la forme u * v avec u = 3 - x et v = 4 + 2*x or (u * v)' = u' * v + u * v'
ça c'est très bien.
Maintenant tu dois écrire directement (ça doit être dans ton cours, ou tu le fais de tête) :
u(x) = -x+3 => u' (x) = -1
v(x) = 2x+4 => v' (x) = 2
donc (uv)' = ...
Maintenant pour calculer une dérivée il vaut mieux utiliser la forme dévelppée (comme suggéré précédemment).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
ça c'est que tu ne connais pas bien ton cours...
(x²)' = 2x
et plus généralement
(x^n)' = n x^(n-1).
mais tu peux terminer comme tu avais commencé. Je t'ai complètement pavé la voie dans mon précédent message.
(x²)' = 2x
et plus généralement
(x^n)' = n x^(n-1).
mais tu peux terminer comme tu avais commencé. Je t'ai complètement pavé la voie dans mon précédent message.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Ta dérivée est fausse. Si tu prends la peine de lire mon message de 09h37 tu verras que je t'ai relancé sur la voie en te donnant toutes les indications.
Par ailleurs tu peux vérifier ton calcul en dérivant -2x²+2x+12 directement avec les rappels que je t'ai fait dans le message de 09h49.
Savoir dériver sera très important (un peu comme savoir développer un produit...) au moins jusqu'au bac et si tu continues à faire un peu de science / d'économie, donc cela vaut le coup de prendre un peu de temps pour comprendre comment ça marche.
Donc
1) reprends ton calcul avec les indications du message 09h37
2) vérifie ton résultat en dérivant directement -2x²+2x+12
Par ailleurs tu peux vérifier ton calcul en dérivant -2x²+2x+12 directement avec les rappels que je t'ai fait dans le message de 09h49.
Savoir dériver sera très important (un peu comme savoir développer un produit...) au moins jusqu'au bac et si tu continues à faire un peu de science / d'économie, donc cela vaut le coup de prendre un peu de temps pour comprendre comment ça marche.
Donc
1) reprends ton calcul avec les indications du message 09h37
2) vérifie ton résultat en dérivant directement -2x²+2x+12
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Etape n°1 : - 2*x ² + 2*x + 12 est de la forme u + v avec u = - 2*x ² et v = 2*x + 12 or (u + v)' = u' + v'
Etape n°2 : - 2*x ² est de la forme u * v avec u = - 2 et v = x ²
or (u * v)' = u' * v + u * v'
Etape n°3 : 2*x + 12 est de la forme u + v avec u = 2*x et v = 12 or (u + v)' = u' + v'
Etape n°4 : 2*x est de la forme ku
or (ku)' = k u' avec k = 2 et u = x
f(x)= -2+2 non ?
Etape n°2 : - 2*x ² est de la forme u * v avec u = - 2 et v = x ²
or (u * v)' = u' * v + u * v'
Etape n°3 : 2*x + 12 est de la forme u + v avec u = 2*x et v = 12 or (u + v)' = u' + v'
Etape n°4 : 2*x est de la forme ku
or (ku)' = k u' avec k = 2 et u = x
f(x)= -2+2 non ?
Bonjour,
alors, plusieurs choses à dire :
1) Quand tu as plusieurs expressions d'une fonction et qu'on te demande sa dérivée, toujours prendre l'expression la plus simple. En l'occurrence, l'expression polynomiale=-2x^2+2x+12) que tu vas pouvoir dériver en une étape. Tu sais que :
que tu vas pouvoir dériver en une étape. Tu sais que : '=n.k.x^{n-1}) avec
avec 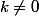 et
et  . A toi de dériver cette fonction maintenant.
. A toi de dériver cette fonction maintenant.
2) pour étudier le tableau de signe d'une fonction affine=ax+b \quad a,b \neq 0)
Le sens de variation de ta fonction dépend du coefficient directeur a : si a > 0, ta fonction est strictement croissante, elle va du négatif au positif. Si a < 0, c'est l'inverse.
L'endroit où elle change de signe, c'est-à-dire,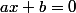 est donné par
est donné par 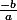
Je vais te donner un exemple pour être plus clair : imaginons qu'après avoir dérivé ta fonction f, tu obtiens=-5x+10) . Tu as
. Tu as 
Le coefficient directeur de ta droite a est négatif donc tu en déduis que ta fonction dérivée est décroissante : elle va du positif au négatif. Et tu sais qu'elle change de signe en (f'(2)=0 donc)
(f'(2)=0 donc)
Tu peux alors construire le tableau de signe de ta dérivée f' : elle est de signe + sur ]-infini,2[ et de signe - sur ]2,+infini[
Après avoir fait ce tableau, tu peux en déduire le tableau de variation de f , qui est croissante là où sa dérivée est de signe + (donc sur ]-infini,2[) et décroissante là où sa dérivée est de signe - (donc sur ]2,+infini[)
alors, plusieurs choses à dire :
1) Quand tu as plusieurs expressions d'une fonction et qu'on te demande sa dérivée, toujours prendre l'expression la plus simple. En l'occurrence, l'expression polynomiale
2) pour étudier le tableau de signe d'une fonction affine
Le sens de variation de ta fonction dépend du coefficient directeur a : si a > 0, ta fonction est strictement croissante, elle va du négatif au positif. Si a < 0, c'est l'inverse.
L'endroit où elle change de signe, c'est-à-dire,
Je vais te donner un exemple pour être plus clair : imaginons qu'après avoir dérivé ta fonction f, tu obtiens
Le coefficient directeur de ta droite a est négatif donc tu en déduis que ta fonction dérivée est décroissante : elle va du positif au négatif. Et tu sais qu'elle change de signe en
Tu peux alors construire le tableau de signe de ta dérivée f' : elle est de signe + sur ]-infini,2[ et de signe - sur ]2,+infini[
Après avoir fait ce tableau, tu peux en déduire le tableau de variation de f , qui est croissante là où sa dérivée est de signe + (donc sur ]-infini,2[) et décroissante là où sa dérivée est de signe - (donc sur ]2,+infini[)
31 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
