Dm
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par Cameliaa.rose-xO » 29 Oct 2012, 14:06
par Cameliaa.rose-xO » 29 Oct 2012, 14:06
Bonjour, j'ai un dm et je bloque sur une question
-etudier les variations de f et dresser son tableau de variation
Comment calculera la derivée de f (x) = (
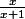
)

? Merci
-
Anonyme
 par Anonyme » 29 Oct 2012, 14:11
par Anonyme » 29 Oct 2012, 14:11
Cameliaa.rose-xO a écrit:Bonjour, j'ai un dm et je bloque sur une question
-etudier les variations de f et dresser on tableau de variation
Comment calculera derivé de f (x) =
}{(x+1)}^3)
? Merci
Bonjour,
Montre-nous comment tu as calculé la derivée s'il te plait, qu'on te dise si c'est juste pour ensuite t'aider pour la suite

-
ExarKun
- Membre Naturel
- Messages: 46
- Enregistré le: 28 Sep 2008, 00:28
-
 par ExarKun » 29 Oct 2012, 14:12
par ExarKun » 29 Oct 2012, 14:12
Bonjour,
' = nu'u^{n-1})
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 29 Oct 2012, 14:13
par ThekamikazeFou » 29 Oct 2012, 14:13
Cameliaa.rose-xO a écrit:Bonjour, j'ai un dm et je bloque sur une question
-etudier les variations de f et dresser son tableau de variation
Comment calculera la derivée de f (x) = (
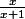
)

? Merci
qu'elle est la dérivée de
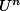
qu'elle est la dérivée de
)
?
il s'agit ici d'une fonction composé :
 ^n w^n)
donc cherche en premier la dérivé de (
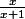
)
 par Cameliaa.rose-xO » 29 Oct 2012, 14:22
par Cameliaa.rose-xO » 29 Oct 2012, 14:22
ThekamikazeFou a écrit:qu'elle est la dérivée de
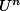
qu'elle est la dérivée de
)
?
il s'agit ici d'une fonction composé :
 ^n w^n)
donc cherche en premier la dérivé de (
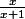
)
Très bien alors merci pour vos réponses
Je trouve ça au début
^2})
=\
Mais c'est le cube qui me gène
-
Anonyme
 par Anonyme » 29 Oct 2012, 14:30
par Anonyme » 29 Oct 2012, 14:30
Cameliaa.rose-xO a écrit:Très bien alors merci pour vos réponses
Je trouve ça au début
^2})
=\
Mais c'est le cube qui me gène
Tu veux dire que le carré au denominateur te gène ?
Alors fais d'abord comme Thekamikazefou t'a proposé, dérives d'abord :
})
 par Cameliaa.rose-xO » 29 Oct 2012, 14:35
par Cameliaa.rose-xO » 29 Oct 2012, 14:35
Saccharine a écrit:Tu veux dire que le carré au denominateur te gène ?
Alors fais d'abord comme Thekamikazefou t'a proposé, dérives d'abord :
})
Non , non je parle du cube de la fonction f(x).
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Oct 2012, 14:37
par Kikoo <3 Bieber » 29 Oct 2012, 14:37
Cameliaa.rose-xO a écrit:Non , non je parle du cube de la fonction f(x).
Salut,
formule de dérivation des fonctions composées
-
Anonyme
 par Anonyme » 29 Oct 2012, 14:39
par Anonyme » 29 Oct 2012, 14:39
Cameliaa.rose-xO a écrit:Non , non je parle du cube de la fonction f(x).
Ah excuse moi, j'ai regardé la formule de ton precedent post, et non de la fonction...
 par Cameliaa.rose-xO » 29 Oct 2012, 15:19
par Cameliaa.rose-xO » 29 Oct 2012, 15:19
Saccharine a écrit:Ah excuse moi, j'ai regardé la formule de ton precedent post, et non de la fonction...
La dérivé de x / x+1 c'est
^2})
mais pour le cube j'en fais quoi ?
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 29 Oct 2012, 15:28
par ThekamikazeFou » 29 Oct 2012, 15:28
qu'elle est la dérivé de u^n ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 29 Oct 2012, 15:31
par maths0 » 29 Oct 2012, 15:31
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 29 Oct 2012, 15:35
par ThekamikazeFou » 29 Oct 2012, 15:35
maths0 a écrit:^3} = {x^3} + 3{x^2} + 3x + 1\\<br />f(x) = {\left( {\frac{x}{{x + 1}}} \right)^3} = \frac{{{x^3}}}{{{x^3} + 3{x^2} + 3x + 1}}<br />\end{array})
cette technique est déconseillé, ça fonctionne mais c'est laborieux et des formules de dérivation simple existe.
imagine que tu ais
 = {\left( {\frac{x}{{x + 1}}} \right)^9})
es tu sur de refaire la même technique ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 29 Oct 2012, 15:37
par maths0 » 29 Oct 2012, 15:37
ThekamikazeFou a écrit:cette technique est déconseillé, ça fonctionne mais c'est laborieux et des formules de dérivation simple existe.
imagine que tu ais
 = {\left( {\frac{x}{{x + 1}}} \right)^9})
es tu sur de refaire la même technique ?
"Newton mon ami" :lol3:
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 29 Oct 2012, 16:04
par ThekamikazeFou » 29 Oct 2012, 16:04
maths0 a écrit:"Newton mon ami" :lol3:
J'aurais plus dis "pascal mon amis" ; :lol3:
 par Cameliaa.rose-xO » 29 Oct 2012, 17:08
par Cameliaa.rose-xO » 29 Oct 2012, 17:08
ThekamikazeFou a écrit:J'aurais plus dis "pascal mon amis" ; :lol3:
Quelle methode est conseiller alors? :/
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 29 Oct 2012, 17:11
par maths0 » 29 Oct 2012, 17:11
Cameliaa.rose-xO a écrit:Quelle methode est conseiller alors? :/
Celle que tu préfères.
 par Cameliaa.rose-xO » 29 Oct 2012, 17:46
par Cameliaa.rose-xO » 29 Oct 2012, 17:46
maths0 a écrit:Celle que tu préfères.
D'accord ,, j'ai compris qu'on a utiliser l'identité remarquable pour le cube mais dans le cas ou on a
 = {\left( {\frac{x}{{x + 1}}} \right)^9})
comment fait-on?
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 29 Oct 2012, 17:53
par ThekamikazeFou » 29 Oct 2012, 17:53
on utilise jamais les identitées remarquables !
u étant une fonction définis sur un intervalle I on a :
(u^n)' = u'u^(n-1)
on ne va pas développé à chaque puissance, on pourrait avec une puissance 9 en utilisant le triangle de pascal, mais c'est très laborieux.
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 29 Oct 2012, 17:57
par maths0 » 29 Oct 2012, 17:57
ThekamikazeFou a écrit:on utilise jamais les identitées remarquables !
u étant une fonction définis sur un intervalle I on a :
(u^n)' = u'u^(n-1)
on ne va pas développé à chaque puissance, on pourrait avec une puissance 9 en utilisant le triangle de pascal, mais c'est très laborieux.
Vaut mieux que ce soit bien fait avec la formule de Newton plutot que mal fait avec une mauvaise formule que l'on ne connait pas :zen:.
La formule (u^n)' = u'u^(n-1) est fausse.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
? Merci
)
? Merci