Dm sur les équations de cercles !!!

[elise84]

Je suis nouvelle sur ce forum et je ne sais pas encore très bien comment ça fonctionne, mais je suis en 1ère S et je commence à avoir besoin d'aide, donc si vous pourriez m'aider ça serait super :we: !

Voilà l'énoncé:

Au réel m, on associe, s'il existe, le cercle Cm d'équation:
x²+y²-2mx-2my+4(m-1)=0 [1]

1)a)Justifiez que [1] s'écrit:
(x-m)²+(y-m)²=2[(m-1)²+1] [2]

b)Déduisez de [2] que, pour tout réel m, Cm est un cercle dont vous préciserez les coordonnées du centre et le rayon en fonction de m.

2)a)Dans le repère (O;i;j), tracez les cercles C0, C1 et C2.
b)Quelle conjecture faites-vous concernant ces trois cercles? Prouvez-la.

3)a)Pour tout réel m, démontrez que Cm passe par deux points fixes A et B que vous préciserez.
b)Pourquoi les centres de Cm sont-ils des points de la droite d'équation y=x ?


Bon la 1)a) j'y suis arriver en dévellopant gràce à la forme canonique !
la 2)b) d'après [2] les coordonées du centre sont (m;m) et le rayon est racine carrée de 2[(m-1)²+1] !
Ensuite j'ai tracé les 3 cercles, mais je ne vois pas la conjecture à faire !!!

Merci de bien vouloir m'aider !
Bonne journée à tous

[Ericovitchi]

Si tu as tracé les 3 cercles, tu as bien dû t'apercevoir qu'ils avaient des points en commun ?

[elise84]

ben justement non :triste: pour la conjecture je pense qu'il y a une symétrie centrale qui apparait mais je vois pas le rapport avec l'exo ni comment le prouver donc je ne pense pas que ce soit ça !

[Ericovitchi]

Alors tu as mal tracé tes cercles car ils passent tous par les points (2,0) et (0,2).

D'ailleurs remplaces x et y par les coordonnées de ces points dans l'équation et tu verras quelle est vérifiée quel que soit m.

[Finrod]

Cherche les points d'intersection de et avec les équations

tu dois trouver qu'il sont sur la droite y=-2-x. Comme seuls deux points de cette droite sont sur , il suffit de vérifier que tous les cercles coupent cette droite pour en déduire qu'il la coupent en ces deux même points.

Pour montrer que tous les cercles coupent la droite, il faut montrer que la distance de leur centre de coordonnée (m,m) à la droite (après calcul, ça fait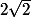 ) est inferieure à leur rayon

ps> Ericovitchi ayant identifié les deux points, il est plus simple de verifier que ces deux points appartiennent bien à chaque cercle.