Soustraire deux inéquations.

[Kugge]

Bonjour, pourquoi est-il impossible de soustraire deux inéquations de même signe ? Est-il possible de soustraire deux inéquations qui ne sont pas de même signe ? Je ne trouve pas d'explications justifiant cette règle
Merci pour vos réponses

[Tuvasbien]

Si je comprends bien la question est pourquoi si 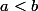et 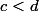on a pas ? Parce qu'avec , on aurait .

[Kugge]

Si je comprends bien la question est pourquoi si et on a pas ? Parce qu'avec , on aurait .

Certes il y a des exemples justifiant cette règle mais, en soi, pourquoi mène-t-elle à une erreur, pourquoi ce résultat est faux ? Je ne sais pas trop si ma demande est compréhensible, je vais essayer de fournir un exemple :

Lorsqu'on utilise les congruences on sait qu'il ne faut pas diviser car on risque de manipuler un réel et non un entier

De même je ne trouve pas d'explications justifiant le fait que l'on doit changer de signe lorsqu'on multiplie une inégalité par un nombre négatif. (Malgré les exemples justifiant cela, je tente juste de comprendre la règle dans son intégralité)

[Kugge]

(L'exemple fourni est le type d' "explication" que je cherche)

[Tuvasbien]

Concernant le changement de sens dans les inégalités, ça vient du fait que la fonction est décroissante sur pour donc si 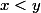, alors (et de même pour le passage à l'inverse etc...). Pour la soustraction je ne sais pas trop, c'est simplement faux, c'est comme le fait que l'intégration conserve les inégalités mais pas la dérivation, ce sont des opérations "inverses" l'une de l'autre mais elles ne se comportent différement avec les inégalités.

[Kugge]

Concernant le changement de sens dans les inégalités, ça vient du fait que la fonction est décroissante sur pour donc si , alors (et de même pour le passage à l'inverse etc...). Pour la soustraction je ne sais pas trop, c'est simplement faux, c'est comme le fait que l'intégration conserve les inégalités mais pas la dérivation, ce sont des opérations "inverses" l'une de l'autre mais elles ne se comportent différement avec les inégalités.

Merci pour cet exemple.
J'ai réfléchis un peu et je me dis qu'une soustraction est simplement une addition mais multipliée par -1, donc les signes ne correspondent plus lorsqu'on vient soustraire deux inégalités. Je pense que ca doit être quelque chose comme ca (basé sur l'exemple que vous m'avez fourni ci dessus)

[GaBuZoMeu]

Ben voila, tu as compris. Et tu as aussi compris pourquoi, si on a 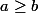et , alors .