Sinus

[line04]

bonjour, j'ai commencée mon DM depuis une bonne semaine mais je reste bloquée à une question pouvez vous m'aider à y voir plus claire s'il vous plaît? merci

Soit f la fonction définie sur [-2;2] par f(x)= 1+3x-x^3

1) a) f'(x)= -3x²+3= 3(-x²+1)
b) théorème de la bijection

jusque là j'y suis arrivée mais à la question 2) on me demande:

On note x1;x2 et x3 ces 3 solutions avec x12) On se propose de déterminer la valeur exacte de x1, x2 et x3 sous la forme 2sin alpha
a) Démontrer que pour i appartient (1,2,3) il existe un seul réel alpha i dans l'intervalle [-pi/2; pi/2] tel que xi=2sin aplha i
b) démontrer que pour tout réel u sin 3u=3sinu-4sin^3u
c) justifier que alpha 1, aplpha 2 et alpha 3 sont solutions de l'équation 1+2sin3u=0
d) résoudre l'équation 1+2sin3u=0 dans l'intervalle [-pi/2; pi/2]
e) conclure


Aidez moi s'il vous plait sans la a) je ne peux pas faire le reste du moins je ne pense pas et je ne sais pas cmment m'y prendre

[line04]

Aidez moi s'il vous plaît je suis completement bloquée je ne sais pas par où commencer ni comment faire!! :cry:

[Ericovitchi]

comme un sinus est toujours entre -1 et +1 pour qu'il existe un angle tel que
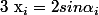
il faut montrer que toutes les racines sont entre -2 et +2
Après on montre que cet angle est unique car le sinus entre -pi/2 et pi/2 est croissant et monotone.

[line04]

je ne vois pas comment faire pour montrer que les racines sont comprises entre -2 et 2

[Ericovitchi]

tu as étudié les variations de la fonction. calcules f(-2) et f(+2) et montres que les zéros de la fonction sont entre ces valeurs.
f(-2) est encore positif donc le premier zéro est après et f(2) est déjà positif donc le 3 ième zéro est juste avant.
(c'est vérifiable d'ailleurs les 3 zéros valent à peu près x~-1.53209 ; x~-0.347296 ; x~1.87939)