Résolution d'inéquation [1ère S]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 10 Fév 2009, 11:16
par Anonyme » 10 Fév 2009, 11:16
Bonjour à tous,
Voilà, j'aimerai savoir comment résoudre cette inéquation.

J'ai essayé diverses choses.
J'ai d'abord essayé de factoriser l'expression.

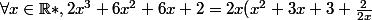)
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 10 Fév 2009, 11:24
par oscar » 10 Fév 2009, 11:24
Bonjour
2x³ + 6x²+ 6x +2 > =0
Grouper ( 2x³ +2) + (6x² +6x) >=0
2( x³ +1) + 6x ( x+1) >= 0
Factorise x³ +1 par la formule a³ +b³ = (a+b)(a²-a+1) puis mettre en évid.
-
Anonyme
 par Anonyme » 10 Fév 2009, 11:40
par Anonyme » 10 Fév 2009, 11:40
Ok. Ne pourrais-je pas faire autrement car la méthode que tu m'a donné n'a pas été vu en cours. Nous avons depuis le début de l'année, très peu travailler sur des inéquations avec du 3ème degré et nous n'avons pas une véritable méthode. J'ai très bien compris ce que t'as marqué et je peux essayé de passer par cette méthode.
Mais chaque fois que nous avons ce genre d'exercice, le professeur nous donne une racine. De là, on peut trouver la factorisation.
Ici, -1 serait une racine (je l'ai trouver grâce à ma calculatrice graphique).
Soit la factorisation : (x+1)(ax²+bx+c) où a,b et c sont à trouver par identification des coefficients...
Je trouve donc : (x+1)(2x²+4x+2)
et la je peux résoudre mon inéquation...
Mais ce n'est pas vraiment très rigoureux, dans la mesure où je me suis aider de ma calculatrice.
Merci pour ton aide.
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 10 Fév 2009, 11:58
par oscar » 10 Fév 2009, 11:58
Re Ta méthode est très valable
Tes résultats sont Bons
Il te reste à mettre x en évidence dans le 2e facteur
On retrouve une formule connue ( a+b)³ = a³ +3a² +3a +1
Par conséquent une autre méthode: mettre x en évidence puis appliquer la fiormule
indiquée
-
Anonyme
 par Anonyme » 10 Fév 2009, 12:01
par Anonyme » 10 Fév 2009, 12:01
Ok merci beaucoup oscar. J'ai réussi. :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 109 invités