Repère orthonormal

[kelly111]

Bonjour, je n'arrive pas à faire le b)

A (1; 3) , B (0; 1) , C (3; - 1) sont trois points du plan muni d'un repère orthonormal.
a) Donner une équation cartésienne de chacune des droites (AB), (BC) et (CA).
b) Soit A1, B1 et C1 les projetés orthogonaux respectifs de A, B et C sur (BC), (CA) et (AB). Donner une équation cartésienne de chacune des droites (AA1), (BB1) et (CC1).
c) En déduire les coordonnées de l'orthocentre H du triangle ABC.

merci d'avance!

[Ben314]

Salut,
Concernant la question b), la "réponse attendue" va dépendre de ce que tu connaît concernant les "équation de droites".
En supposant que tu connaisse uniquement les équation de la forme où est "la pente" (ou "le coefficient directeur") de la droite alors la "règle", c'est que deux droites sont orthogonale lorsque le produit des coefficients directeurs fait -1.

Exemple : On cherche la droite passant pas et orthogonale à la droite d'équation .
Soit l'équation de . Comme est orthogonale à on a c'est à dire et l'équation est de la forme . Pour que soit sur il faut que donc que .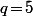
La droite cherchée a donc pour équation .

[Elias]

Salut,

Je pense plutôt que l'élève en question est en 1ère S au chapitre "applications du produit scalaire" et qu'il a vu la notion de vecteur normal à une droite.
L'équation y=mx+p est plutôt appelée équation réduite et non équation cartésienne de la droite.


Donc étant donnée une droite dont une équation cartésienne est ax+by+c=0, le vecteur de coordonnées (a, b) est un vecteur normal à cette droite.

[kelly111]

Bonjour,
Je suis en 2nde !
je n'ai donc pas vu le produit scalaire !
désolé de ne pas avoir mis cette information avant !

[kelly111]

Exemple : On cherche la droite passant pas et orthogonale à la droite d'équation .
Soit l'équation de . Comme est orthogonale à on a c'est à dire et l'équation est de la forme . Pour que soit sur il faut que donc que .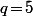
La droite cherchée a donc pour équation .[/quote]


Bonjour, merci pour votre réponse je vais essayer avec l'aide de votre exemple!