Recurrence......help!!!
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 16:04
par mostdu95 » 05 Jan 2007, 16:04
bonjour
je dois montrer par récurrence que :
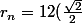^{n+1})
avec

(

j'ai fait l'innitialisation ( je trouve que c' est vraie au rong n =0 ) j'ai fait également l'hypothese de récurrence; en fait je me bologue surtout dns l'étape qui suit i.e j'arrive po à démontrer que c'est vraie au rong n+1
merci d'avance
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 05 Jan 2007, 16:29
par anima » 05 Jan 2007, 16:29
mostdu95 a écrit:bonjour
je dois montrer par récurrence que :
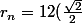^{n+1})
avec

(

j'ai fait l'innitialisation ( je trouve que c' est vraie au rong n =0 ) j'ai fait également l'hypothese de récurrence; en fait je me bologue surtout dns l'étape qui suit i.e j'arrive po à démontrer que c'est vraie au rong n+1
merci d'avance
Reprenons:
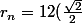^{n+1})
à prouver

avec
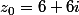
1) Rang 0: |6+6i| =
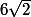
Formule:
^{-n-1}=12\sqrt{2}/2=6\sqrt{2})
Vrai au rang 0
2) Je vais faire une simplification à ta formule, qui va te montrer pourquoi t'avais des problèmes:
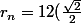^{n+1}\\<br />= 12(\frac{1}{\sqrt{2}})^{n+1}\\<br />= 12(\sqrt{2}^{-1})^{n+1}\\<br />= 12(\sqrt{2})^{-n-1})
C'est plus agréable comme ça, non? Donc, si tu comprends ta récurrence, à chaque rang, tu divise par 1/sqrt(2). Direction la preuve:
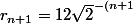-1}\\<br />=12\sqrt{2}^{-n-2}\\<br />= 12\sqrt{2}^{-n-1}\sqrt{2}^{-1}\\<br />= r_n \times \sqrt{2}^{-1})
Ca s'appelle une preuve valide, je pense...
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 16:53
par mostdu95 » 05 Jan 2007, 16:53
d'accord anima ; mais est ce que le fait d'avoir prouver que
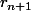
=

suffit pour dire que c'est vraie au rong n+1 donc c'est vrai^por tt n
par ce que moi j'avais pas tronsformé
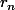
et du coup j'ai montré que

et j'etait pas sûr ?
CAR ON DOIT MONTRER QUE
^{n+2})
et nous on est partait du fait qu'il y est deja ça
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 05 Jan 2007, 17:09
par anima » 05 Jan 2007, 17:09
mostdu95 a écrit:d'accord anima ; mais est ce que le fait d'avoir prouver que
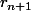
=

suffit pour dire que c'est vraie au rong n+1 donc c'est vrai^por tt n
par ce que moi j'avais pas tronsformé
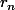
et du coup j'ai montré que

et j'etait pas sûr ?
CAR ON DOIT MONTRER QUE
^{n+2})
et nous on est partait du fait qu'il y est deja ça
Effectivement...Tu as une expression de
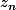
?
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 17:11
par mostdu95 » 05 Jan 2007, 17:11
bahh non...!!!!!!!!!!!!!!!!! on connait juste son module
je demondais jucte est ce que t' a demo est fini ??
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 05 Jan 2007, 17:16
par anima » 05 Jan 2007, 17:16
mostdu95 a écrit:bahh non...!!!!!!!!!!!!!!!!! on connait juste son module
je demondais jucte est ce que t' a demo est fini ??
Alors comment es-tu sensé faire? Tu n'as que le rang zéro comme crible! :hum:
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 17:18
par mostdu95 » 05 Jan 2007, 17:18
J'ai pas compri :triste:
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 05 Jan 2007, 17:21
par anima » 05 Jan 2007, 17:21
mostdu95 a écrit:J'ai pas compri :triste:
Dans un raisonnement par récurrence "normal", on te dit, je vais prendre l'exemple de la somme des entiers naturels:
Prouver que 1+2+3+4+...+n=n(n+1)/2.
Tu as les deux côtés de l'équation: l'équivalent algébrique de la formule, et la logique entre les étapes. Or, dans ton cas, tu n'as que la formule, et un malheureux crible en rang zéro. On sait que

, mais quelle est l'expression de
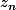
, pour pouvoir trouver le crible en question pour le rang n+1? Ton exercice fait-il partie d'un plus grand exo?
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 17:22
par mostdu95 » 05 Jan 2007, 17:22
oui oui c'est vrai
c'est la partie B ça
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 05 Jan 2007, 17:25
par anima » 05 Jan 2007, 17:25
mostdu95 a écrit:oui oui c'est vrai
c'est la partie B ça
Et...dans la partie a...As-tu la formule pour
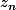
?
[B]P.S:[/TEX] j'ai essayé de trouver et prouver une formule pour
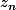
sachant que l'argument doit rester identique (donc le complexe va être de la forme k(1+i)), et k doit valider
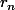
donné. On trouve
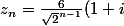)
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 17:25
par mostdu95 » 05 Jan 2007, 17:25
en fait j'ai

avec
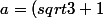/4 +i({sqrt3}-1/4)
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 17:30
par mostdu95 » 05 Jan 2007, 17:30
j'ai l'expression de

-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 05 Jan 2007, 17:37
par anima » 05 Jan 2007, 17:37
mostdu95 a écrit:en fait j'ai

avec
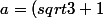/4 +i({sqrt3}-1/4)
La culasse se débloque, d'un coup.
Trouvé, prouvé
On prendra donc comme formule pour
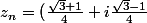^n(6+6i))

Ca va saigner sec, alors accroche-toi. Si tu ne comprends pas une étape, dis-moi et j'expliquerai.
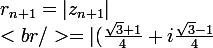^{n+1}(6+6i)|\\<br />=|(\frac{\sqrt{3}+1}{4}+i\frac{\sqrt{3}-1}{4})^n(6+6i)(\frac{\sqrt{3}+1}{4}+i\frac{\sqrt{3}-1}{4})|)

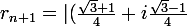^n(6+6i)||(\frac{\sqrt{3}+1}{4}+i\frac{\sqrt{3}-1}{4})|\\<br />= 12\sqrt{2}^{-n-1}|(\frac{\sqrt{3}+1}{4}+i\frac{\sqrt{3}-1}{4})|\\<br />= 12\sqrt{2}^{-n-1} \times \sqrt{(\frac{\sqrt{3}+1}{4})^2+\frac{\sqrt{3}-1}{4})^2}\\<br />= 12\sqrt{2}^{-n-1} \times \sqrt{\frac{1}{2}}\\<br />= 12\sqrt{2}^{-n-1} \times \sqrt{2}^{-1}\\<br />= 12\sqrt{2}^{-n-2})
PROUVED! :doh:
(Les raisonnements par récurrence, c'est comme le vélo. Plus on en fait, plus on sait en faire. Et une fois que c'est appris, ca ne s'oublie plus; la preuve en image: j'ai fait les suites en novembre l'an dernier :we: )
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 17:45
par mostdu95 » 05 Jan 2007, 17:45
t ' sais quoi .......... :++: :++: je te couronne
j' ai bien compris ,; une petite précicion :
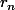
est une suite géométrique de raison

et de premier terme 12 OU 6

c'est ça ?
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 05 Jan 2007, 17:47
par anima » 05 Jan 2007, 17:47
mostdu95 a écrit:t ' sais quoi .......... :++: :++: je te couronne
j' ai bien compris ,; une petite précicion :
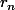
est une suite géométrique de raison

et de premier terme 12 OU 6

c'est ça ?
Premier terme 6racine(2).
:id2: :go: :king2:
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 17:51
par mostdu95 » 05 Jan 2007, 17:51
mmmmmmeeeeeerrrrrrccccccccci
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 22:18
par mostdu95 » 05 Jan 2007, 22:18
y a encore un truc anima; comment tu passe de |
/4+i({sqrt3}-1)/4)^{n} (6+6i})
| à 12
^{-n-1})
car tout à l'heure j'avais pas refais les calcules et là moi je trouve plutôt
^{n} \times6{sqrt2})
:doh:
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 05 Jan 2007, 22:19
par anima » 05 Jan 2007, 22:19
mostdu95 a écrit:y a encore un truc anima; comment tu passe de |
/4+i({sqrt3}-1)/4)^{n} (6+6i})
| à 12
^{-n-1})
car tout à l'heure j'avais pas refais les calcules et là moi je trouve plutôt
^{n} \times6{sqrt2})
:doh:
Si la propriété est vraie au rang n alors elle est vraie au rang n+1. Or, au rang n, |
/4+i({sqrt3}-1)/4)^{n} (6+6i})
|=

-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 22:21
par mostdu95 » 05 Jan 2007, 22:21
ahh oui oui en effet d'aprés l'hypothese de récurrence on remplace l'expression par celui de r_n
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 05 Jan 2007, 22:22
par mostdu95 » 05 Jan 2007, 22:22
:king2: ( :ruse: et là c'est définitivement...!!! :ptdr: )
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
