DM : Question sur deux inéquations

par **nicoak69** » 07 Mar 2010, 19:05

Bonjour, je n'arrive pas à réussir les inéquations (pour faire un tableau de signe) suivantes :
1/(x-3)²">ou égal" à 1
En fait, il faudrait faire perdre le "²" pour que je trouve une fraction du type "ax+b/cx+d"

La deuxième est une inéquation du second degré qu'il faudrait que je change en inéquation du premier degré (comme on a pas vu le second degré), la voilà :
x²+2x+1/4">ou égal" à 0
On donne l'information x²+2x= (x+1)²-1
Pour cette inéquation, pour l'instant, je trouve : (x)(x+2)+1/4>0, il faudrait "faire perdre" le 1/4 pour que je puisse faire mon tableau de signe

Si je n'ai pas été clair merci de me le signaler

Si quelqu'un pourrait me donner le "coup de pouce" qui fait avancer les choses.... merci bien !
PS: Désolé je ne connais pas bien le système de codage pour écrire les fractions...

par **Sa Majesté** » 07 Mar 2010, 19:58

Pour la 1ère

tu peux faire passer le 1 de l'autre côté

et utiliser une identité remarquable

par **nicoak69** » 07 Mar 2010, 20:00

Merci ton aide m'est utile !

par **Sa Majesté** » 07 Mar 2010, 20:03

Quelle identité utilises-tu ?

par **nicoak69** » 07 Mar 2010, 20:10

J'utilise (a+b)(a-b) alors je trouve (x-2)(-x-2)/(x-3)² mais comment faire perdre le "²" au "(x-3)²" ?

par **Als128** » 07 Mar 2010, 20:16

Ben disons que maintenant tu t'es efforcé de transformer ton inégalité en une inégalité par rapport à 0 (à savoir : est-ce que mon expression est positive ou négative) Le fait que (x-3) soit au carré est plutôt une bonne nouvelle : il sera toujours positif (ou nul, mais dans ce cas l'expression n'est plus définie)

Le signe de ton expression revient à étudier le signe du numérateur...

par **nicoak69** » 07 Mar 2010, 20:24

Als128 a écrit:Ben disons que maintenant tu t'es efforcé de transformer ton inégalité en une inégalité par rapport à 0 (à savoir : est-ce que mon expression est positive ou négative) Le fait que (x-3) soit au carré est plutôt une bonne nouvelle : il sera toujours positif (ou nul, mais dans ce cas l'expression n'est plus définie)

Le signe de ton expression revient à étudier le signe du numérateur...

Le signe du numérateur ? Comment ça ?

En fait je viens de comprendre que je peux garder le carré en bas pour le tableau de signe... mais mon numérateur (x-2)(-x-2) est juste ?

par **nicoak69** » 07 Mar 2010, 20:27

*A compris :we: *

Et pour le x²+2x+1/4>0 quelqu'un peut me venir en aide ?

par **Als128** » 07 Mar 2010, 20:32

non car

et non -x-2

Mais pour la première inéquation tu pouvais également dire que

c'est la même chose

et ça te simplifiait la tache....

par **nicoak69** » 07 Mar 2010, 20:40

Ah merci beaucoup !
Mais par contre je suis bloqué pour le deuxième éxercice... si tu as un coup de main à me donner...

par **Als128** » 07 Mar 2010, 20:47

nicoak69 a écrit:On donne l'information x²+2x= (x+1)²-1
Pour cette inéquation, pour l'instant, je trouve : (x)(x+2)+1/4>0, il faudrait "faire

Je pense surtout que tu devrais te servir de l'indication et remplacer

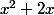
par l'indication qu'on te donne... tu devrais tomber rapidement sur une identité remarquable facile à factoriser...

par **nicoak69** » 07 Mar 2010, 20:51

Oui en faisant ça, voici ce que je trouve :
x²+2x+1/4>0
= (x+1)²-1+1/4>0
= (x+1-1)(x+1+1)+1/4>0
= (x)(x+2)+1/4>0
Et ici je suis bloqué, alors est-ce que j'ai mal utilisé l'identitée ?

par **nicoak69** » 07 Mar 2010, 20:57

Parceque en fait pour mon tableau de signe il me faudrait une expression du type : (...)(...) donc le "+1/4" me gêne un peu

par **Als128** » 07 Mar 2010, 20:59

et si au lieu de developper

tu t'interessais à

...

par **nicoak69** » 07 Mar 2010, 21:12

1/4-1 = -3/4
j'aurai donc : (x+1)²-3/4
là je vois qu'une seule solution : factoriser avec (a+b)(a-b) mais 3/4 est le carré de V(pour racine carrée désolé)3/2 et ça m'aide pas avec la racine carrée, tu n'as pas une petit coup de main de plus à me donner ?

par **Als128** » 07 Mar 2010, 21:17

qu'est ce qui t'aide pas ?
tu trouve un produit qui doit être positif... c'est à dire que c'est plus facile pour tes solutions (que ce soit racine carré ou non...) ca te donnera :(x+1-V(3)/2)(x+1+V(3)/2)>=0

Il est ou le pbl ?

par **nicoak69** » 07 Mar 2010, 21:21

Justement je vois pas de pb, mais juste ça m'étonnerait que ma prof me refasse utiliser les racines mais si tu es sûr de toi, merci vraiment tu me sauves la mise !

Je te revaudrai ça ! *se croit dans un film*
Merci encore !

par **nicoak69** » 07 Mar 2010, 21:28

Euh, encore moi :
donc si j'ai bien compris au final j'ai :
(x+2-V(3)/2)(x+2+V(3)/2) ?

par **Als128** » 07 Mar 2010, 21:40

pourquoi +2 ?

par **nicoak69** » 07 Mar 2010, 21:41

Parceque ma calculatrice me l'a dit elle di exactement :
2+V3
-----
2
donc logiquement comme il reste x je mets +2 tu as une autre solution ?

DM : Question sur deux inéquations

DM : Question sur deux inéquations

Qui est en ligne