Pyramide base carrée

[tommyKM]

Bonjour,
Je suis actuellement en 1er S et j’ai quelques difficultés à résoudre un problème de maths. J’ai des pistes mais je n’aboutis à rien, alors si vous pouviez m’aiguiller un petit peu svp, ça ne serait pas de refus ^^
Voici l’énoncé :
« On veut construire une tente en forme de pyramide à base carrée, soutenue par un poteau au centre. On désigne par A le nombre de m² de toile disponible afin de fabriquer les 4 faces de la tente. »
Retrouver l’expression du volume V(x) de la tente en fonction de la longueur x du côté de la base tel que : V(x) = 1/6 x (√(A^2-x^4 )
Déterminer la longueur x de la base de la tente ainsi que la hauteur h du poteau central pour que V(x) soit maximal
Pour le a), je sais que le volume d’une pyramide à base carré de longueur x et de hauteur h est :
V = 〖hx〗^2/3, à partir de ceci, j’ai essayé d’introduire A mais je ne vois pas comment, le seul paramètre sur lequel je peux jouer, c’est h mais en l’exprimant en fonction de x avec Pythagore, je ne retrouve pas un résultat proche du leur.
Pour le b), il suffit de de dériver V(x) et de trouver son extremum mais là encore, j’ai des formes à rallonge qui ne donnent rien.

[Ben314]

Salut,

Pour le a), je sais que le volume d’une pyramide à base carré de longueur x et de hauteur h est : V = 〖hx〗^2/3

Déjà, je comprend pas trop ta formule : c'est V=((hx)^2)/3 comme tu l'a écrit ou bien V=(hx)^(2/3) ?
Ensuite, dans les deux cas, c'est complètement et totalement débile ton truc : si x et h sont en mètres alors xh est en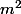 et, si c'est la formule ((hx)^2)/3 ça fait des 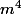ce qui est complètement incohérent pour un volume et, si c'est la formule (hx)^(2/3) ça fait des ce qui est tout aussi incohérent (Rappel : un volume, c'est évidement en 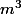que ça se mesure !!!)

V = 〖hx〗^2/3, à partir de ceci, j’ai essayé d’introduire A mais je ne vois pas comment...

Ben, l'énoncé te dit que A est la surface de toile et, évidement, ça s'exprime en fonction du coté x de la base et de la hauteur h. Et une fois que tu as A en fonction de x et h, faut évidement en déduire h en fonction de x et de A vu que ta formule à démontrer contient du x, du A, mais pas de h.

Ensuite, y'aura plus qu'à "injecter" ça dans la formule (juste...) qui donne la volume en fonction de x et de h pour avoir comme demandé le volume en fonction de x et A.

[tommyKM]

Oui dsl mais c'était V=(h*x²)/3, comme cela, c'est un peu plus cohérent.
Du coup, je viens d'exprimer A tel que A=4*[(x*h)/2] puisqu'on a 4 faces soit A=2*x*h
Donc cela me donne h= A/(2*x)
Par contre, lorsque j'injecte h dans V(x), cela me donne V(x)=(1/6)*x*A, ce qui est différent du résultat voulu, il manque la racine mais je ne vois pas où je me suis trompé !

[Ben314]

C'est nettement mieux et au niveau du principe, c'est nikel.

Sauf que les 4 triangles qui constituent les 4 cotés de la tente, ils on bien une "base" égale à x, mais par contre leur hauteur, c'est pas h :

Si on note S le sommet de la pyramide (= le haut du poteau central), O le projeté orthogonale de S sur la base ( = le bas du poteau central) et M le milieu d'un des 4 cotés formant la base (fait un dessin...) alors le triangle SOM est rectangle en O et la hauteur que tu cherche (celle des triangles formant les cotés), c'est la longueur SM.

Comme OS=h et que OM=x/2, la formule de Pythagore te donne la longueur SM en fonction de x et de h.

[tommyKM]

C'est bon pour la 1ère question mais par contre la deuxième, lorsque je dérive V(x) j'obtiens une forme à rallonge pas très manœuvrable pour trouver l'extremum !! Une piste ?

[Ben314]

Ben je pense pas qu'il y ait franchement de piste, à part d'essayer de pas se gourrer dans le calcul de la dérivée, ni dans la factorisation de cette dérivée ensuite (pour étudier son signe).
Normalement, le résultat final est par archi pourri : tu doit trouver