Pti blèm! (fraction = 0)

[fabi39]

Je part d'une équation j'arrive à e^x(-1/x² + (kx+1)/x) (c'est la dérivée d'une fonction) et je cherche f'= 0
Bon ben j'ai réduit au même dénominateur ça me fait :
e^x ((-1+kx²+x)/x²) =0 (f'=0)

Donc ça sannule pour e^x=0 (ce qui est impossible) et pour la fraction = 0

Mais la fraction ça me donne :
-1+kx²+x/x² = 0

On peu considérer que le premier est un trinome mais bon..comment faire avec le k? (qui est négatif ou nul d'après l'énoncé)
Comment poursuivre?

[raito123]

Bonjours,
supposant que ce que tu as trouver est juste et le dénominateur est e^x ((-1+kx²+x)/x²)
alors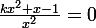
alors kx²+x-1=0 tu n'as que calculer le delta=1+4k et tu calcule selon k si k est potitive alors f' s'annule deux fois.
Si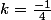 alors ta fonction s'annule une fois.
Si alors ta fonction ne s'annule pas et elle est toujours négative