Problème sur une inéquation Term

[haricot29]

bonsoir tout le monde !
voila je bloque sur une inéquation qui est la suivante :
2x+3+racine(x²-1) >ou= 0
<=> 2x+3 >ou= - racine(x²-1)
<=> 4x²+12x+9 >ou= x²-1
<=> 3x²+12x+10 >ou=0
on calcul delta = b² -4ac
= 12²-4*10*3 = 24
deux racines :
x1 = -b-racine(delta)/2a = -12-racine(24) / 6 = -12-2racine(6)/6
x2 = -b+racine(delta)/2a = -12+2racine(6)/6

Est ce que jusque la c'est ok ?! :id:
Un peu d'aide serait la bienvenue...
MERCI D'AVANCE :doh:

[anima]

bonsoir tout le monde !
voila je bloque sur une inéquation qui est la suivante :
2x+3+racine(x²-1) >ou= 0
2x+3 >ou= - racine(x²-1)
4x²+12x+9 >ou= x²-1
3x²+12x+10 >ou=0
on calcul delta = b² -4ac
= 12²-4*10*3 = 24
deux racines :
x1 = -b-racine(delta)/2a = -12-racine(24) / 6 = -12-2racine(6)/6
x2 = -b+racine(delta)/2a = -12+2racine(6)/6

Est ce que jusque la c'est ok ?! :id:
Un peu d'aide serait la bienvenue...
MERCI D'AVANCE :doh:

Je suis d'accord avec les racines. l'expression est donc du signe de a entre les racines, cad positif?

[haricot29]

2x+3+racine(x²-1) >ou= 0
<=> 2x+3 >ou= - racine(x²-1)
<=> 4x²+12x+9 >ou= x²-1
<=> 3x²+12x+10 >ou=0
on calcul delta = b² -4ac
= 12²-4*10*3 = 24
deux racines :
x1 = -b-racine(delta)/2a = -12-racine(24) / 6 = -12-2racine(6)/6
x2 = -b+racine(delta)/2a = -12+2racine(6)/6

dc aprés cela je fais un tableau de signe , positif entre les 2 racines soit l'ensemble de solution est S = [-12-2racine(6)/6 ; -12+2racine(6)/6]

C'est Ok ?!

[anima]

2x+3+racine(x²-1) >ou= 0
2x+3 >ou= - racine(x²-1)
4x²+12x+9 >ou= x²-1
3x²+12x+10 >ou=0
on calcul delta = b² -4ac
= 12²-4*10*3 = 24
deux racines :
x1 = -b-racine(delta)/2a = -12-racine(24) / 6 = -12-2racine(6)/6
x2 = -b+racine(delta)/2a = -12+2racine(6)/6

dc aprés cela je fais un tableau de signe , positif entre les 2 racines soit l'ensemble de solution est S = [-12-2racine(6)/6 ; -12+2racine(6)/6]

C'est Ok ?!

Ouip. Tu devrais pas avoir trop de problèmes. Au fait, simplifie les racines par 2

[haricot29]

Merci bcp, par contre je ne suis pas une pro de la simplification de racine alr... :doh:

[Quidam]

Attention !
L'inéquation nest pas équivalente à
La preuve :
a pour solution l'intervalle
soit a pour solution

Pour les équations ---> mais la réciproque n'est pas vraie. Pour les inéquations, de on ne peut rien déduire du tout ! Et en particulier, certainement pas que serait supérieur ou égal à !
C'est pourtant ce que tu fais quand tu dis :

[ 2x+3 >ou= - racine(x²-1)] [4x²+12x+9 >ou= x²-1]

[anima]

Attention !
L'inéquation nest pas équivalente à
La preuve :
a pour solution l'intervalle
soit a pour solution

Pour les équations ---> mais la réciproque n'est pas vraie. Pour les inéquations, de on ne peut rien déduire du tout ! Et en particulier, certainement pas que serait supérieur ou égal à !
C'est pourtant ce que tu fais quand tu dis :

[ 2x+3 >ou= - racine(x²-1)] [4x²+12x+9 >ou= x²-1]

Ma calculette m'a pourtant (après avoir martelé comme un bourrin les parenthèses) démontrer par a et b que ses racines étaient justes pour l'équation INITIALE. Ce qui me dit donc que oui, peut-être que descendre au carré implique une dualité des racines. Mais quand même, ça marche dans ce cas...

[Quidam]

Ma calculette m'a pourtant (après avoir martelé comme un bourrin les parenthèses) démontrer par a et b que ses racines étaient justes pour l'équation INITIALE. Ce qui me dit donc que oui, peut-être que descendre au carré implique une dualité des racines. Mais quand même, ça marche dans ce cas...

Je ne parle pas des racines de l'équation mais des solutions de l'inéquation ! Il va sans dire que l'inéquation a des solutions qui font intervenir peu ou prou les racines de l'équation . Mais tout est question d'interprétation de ces fameuses solutions de l'équation pour trouver les solutions de l'inéquation !

Selon haricot29 l'ensemble des solutions est donné par : S = [-12-2racine(6)/6 ; -12+2racine(6)/6]

Comment se fait-il alors que 1000, qui ne fait à l'évidence pas partie de cet intervalle, soit effectivement solution de "2x+3+racine(x²-1) >ou= 0" ?

Eh oui !

2*100+3+racine(999999) > 0

D'ailleurs, l'intervalle donné par haricot29 est entièrement composé de nombres négatifs ; sans aller chercher si loin, 1,2,3 sont solutions de l'inéquation !

2*1+3+racine(0)>=0
2*2+3+racine(3)>=0
2*3+3+racine(8)>=0

Dis moi si j'ai tort !

[haricot29]

k alors mon exo est tout faux ? Ou dois je faire ma correction ?! Merci de me rep .. :doh: :doh:

[Quidam]

k alors mon exo est tout faux ? Ou dois je faire ma correction ?! Merci de me rep .. :doh: :doh:

Ce n'est pas certain que j'aurai le temps ce soir, mais demain sans faute !

[Quidam]

Voici comment je traiterais le problème.

On doit résoudre l'inéquation :

Il faut tout d'abord que la racine soit définie, donc que . Il faut a priori exclure l'intervalle
]-1,+1[.

On se place tout d'abord dans la zone où , soit pour

Alors, il est clair que -2x-3 est négatif ou nul et comme est lui positif ou nul forcément !
Cela nous donne donc déjà toute la zone de à 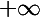comme solution, d'où l'on doit bien sûr retirer la zone où la racine n'est pas définie, c'est-à-dire l'intervalle ]-1,+1[. Donc pour cette zone où on a pour solutions

Voyons à présent le reste : la zone où

Les deux expressions de gauche sont positives. Et on peut dire que
On tombe alors sur les expressions que tu as trouvées :




Ceci se résoud classiquement : si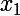 et sont les deux racines de ce trinôme, avec , on trouve :




Le trinôme est négatif où nul pour .

Mais nous nous sommes restreint à la zone où et comme , la solution de notre problème dans la zone où se réduit à l'intervalle

L'ensemble des solutions de notre problème est la réunion des solutions obtenues dans la zone où et de celles obtenues dans la zone où :



J'ai envisagé d'étudier la fonction f définie par pour résoudre le problème, mais la dérivée f ' de cette fonction est du même genre et étudier son signe pose exactement le même type de problème qu'étudier le signe de f : cela n'avance donc à rien.

On peut cependant vérifier l'exactitude de cette solution en tracant le graphe de la fonction f. On constate effectivement que la courbe semble couper une seule fois l'axe des x en un point d'abscisse . J'ai également tracé sur le même graphique la fonction définie pas g(x)=2x+3 en rouge.



Je rappelle une règle essentielle, euh, plutôt l'absence essentielle d'une règle :

Aucune règle ne dit que A fortiori, Aucune règle ne dit non plus que Ceci est FAUX !

Par contre on démontre que si , cela implique que mais la réciproque est fausse.

[haricot29]

Lol non mais sérieux j'étais sur ce DM tt le week et j'ai rien réussi quoi sur 3 exos j'ai est fait un et encore vs etes entrain de me dire que il est pi etre faux Mouhahahz keske je fou en term S ma parole :briques: :briques:

Merci bcp quidam !! Il ne me reste plus que 2 exercice plus durs que celui la a faire mais sinon tout baigne !! :doh: :doh:

[Quidam]

keske je fou en term S ma parole :briques: :briques:

Il ne faut pas te décourager ! Il te suffit de bien apprendre les règles de calcul et cela ne se reproduira plus. Cet exercice peut être qualifié de "difficile" et je ne serais pas étonné que la majorité des élèves de ta classe n'aient pas réussi non plus.

Rappel des règles principales de calcul :

, si C est différent de zéro.
, quel que soit C (même s'il est nul ; mais si C=0, ça ne t'avance à rien !)
, quel que soit C.
, mais attention la réciproque est fausse.

, si C est strictement négatif.
, quel que soit C.
.

Tu dois te débrouiller avec ça !

En fait, c'est normal ! Le but de ce site est d'aider les participants à progresser en maths ! Je suis certain que désormais, tu ne fera plus jamais l'erreur que tu as faite. Donc, c'est parfait ! La prochaine fois, on ne t'y reprendra pas !

Courage !