Problème résolution équation simple
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Aktar
- Membre Naturel
- Messages: 55
- Enregistré le: 14 Avr 2009, 17:30
-
 par Aktar » 15 Nov 2010, 12:04
par Aktar » 15 Nov 2010, 12:04
Bonjour,
J'ai une correction mais je ne suis pas sur qu'elle soit correcte.
si s/p = k/k^a
alors k = (s/p)^(1/(1-a))
êtes vous d'accord ? je n'arrive pas à trouver cette solution.
merci

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 15 Nov 2010, 12:17
par eratos » 15 Nov 2010, 12:17
Si s/p=k/k^a
k=(s/p).k^a= (sk^a)/p tout simplement
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Nov 2010, 12:31
par Arnaud-29-31 » 15 Nov 2010, 12:31
Salut,
Oui c'est juste.
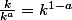
Tu as donc
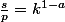
donc
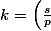^{\frac{1}{1-a}})
pourvu que a soit différent de 1.

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 15 Nov 2010, 13:07
par eratos » 15 Nov 2010, 13:07
C'est chaud! J'avais jamais vu ça.
Si

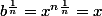
?
-
Aktar
- Membre Naturel
- Messages: 55
- Enregistré le: 14 Avr 2009, 17:30
-
 par Aktar » 15 Nov 2010, 13:44
par Aktar » 15 Nov 2010, 13:44
16 = 4^(2)
16^(1/2)=4
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Nov 2010, 14:09
par Arnaud-29-31 » 15 Nov 2010, 14:09
Oui, une puissance 1/2 correspond à une racine carré.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Nov 2010, 14:11
par Arnaud-29-31 » 15 Nov 2010, 14:11
eratos a écrit:C'est chaud! J'avais jamais vu ça.
Si

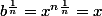
?
Ca n'a rien de chaud, tu as vu en seconde que
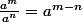
et que
^n = a^{mn})
, je n'utilise rien de plus.
-
Aktar
- Membre Naturel
- Messages: 55
- Enregistré le: 14 Avr 2009, 17:30
-
 par Aktar » 15 Nov 2010, 14:52
par Aktar » 15 Nov 2010, 14:52
Arnaud-29-31 a écrit:Salut,
Oui c'est juste.
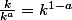
Tu as donc
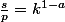
donc
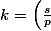^{\frac{1}{1-a}})
pourvu que a soit différent de 1.
ok mais si j'ai par exemple :
(k ^(1/3)) / k = 3/20
je n'ai pas k^(1/3 - 1) = 3/20
qui donne k = 3/20^(1/(-2/3)) ?
je pense que c'est faux mais je ne sais pas pourquoi.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 15 Nov 2010, 15:21
par Ericovitchi » 15 Nov 2010, 15:21
si si c'est bon k = (3/20)^(-3/2) pourquoi doutes tu ?
-
Aktar
- Membre Naturel
- Messages: 55
- Enregistré le: 14 Avr 2009, 17:30
-
 par Aktar » 15 Nov 2010, 15:39
par Aktar » 15 Nov 2010, 15:39
Ericovitchi a écrit:si si c'est bon k = (3/20)^(-3/2) pourquoi doutes tu ?
d'accord mais a est bien égal à 1 dans ce cas.
par contre quand tu as en puissance 1/(-2/3) c'est comme si tu avais -3/2 ? tu passes simplement le 3 au numérateur ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 15 Nov 2010, 15:47
par Ericovitchi » 15 Nov 2010, 15:47
oui A/(B/C)= AC/B ou 1/(A/B)=B/A
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 15 Nov 2010, 15:50
par Sylviel » 15 Nov 2010, 15:50
Non a n'est pas égal a un car dans un cas tu as

dans l'autre

...
Bien sûr si deux fractions sont égales elle le sont aussi quand on les mets dans une puissance. Est-ce qu'il te viendrait à l'esprit de demander : "est ce que a^{1+1}=a^2" ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Aktar
- Membre Naturel
- Messages: 55
- Enregistré le: 14 Avr 2009, 17:30
-
 par Aktar » 15 Nov 2010, 16:21
par Aktar » 15 Nov 2010, 16:21
ok merci.
J'ai un autre problème avec ma correction :
la dérivée de (a/b)^(1/(1-c))
donne c . (a/b)^((c-1)/(1-c))
je ne comprend pas cette formule, mes corrections ne sont pas assez détaillées.
et si on pose c . (a/b)^((c-1)/(1-c)) - b = 0
alors a=c ?
merci pour votre aide précieuse
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
 dans l'autre
dans l'autre  ...
...