Problème maths pyramide
17 messages
- Page 1 sur 1
Problème maths pyramide
Bonsoir à tous,
J'ai un dm de maths à faire et je n'arrive pas à le résoudre. J'aurai besoin de votre aide ! Le voici :
SABCD est une pyramide à base rectangulaire
(ABCD --> base et S sommet de la pyramide)
On sait que SA=4, SB=5, SC=6.
Trouver combien vaut SD.
(On ne connaît pas la hauteur ni combien vaut les côtés de la base)
Merci d'avance pour votre aide !
J'ai un dm de maths à faire et je n'arrive pas à le résoudre. J'aurai besoin de votre aide ! Le voici :
SABCD est une pyramide à base rectangulaire
(ABCD --> base et S sommet de la pyramide)
On sait que SA=4, SB=5, SC=6.
Trouver combien vaut SD.
(On ne connaît pas la hauteur ni combien vaut les côtés de la base)
Merci d'avance pour votre aide !
Re: Problème maths pyramide
Salut,
Ca me semble un peu bizarre qu'on puisse conclure avec aussi peu d'information (tu as rien d'autre ?)
Si on prend un repère centré en D et dont les eux premier axes sont les droites (DA) et (DC) alors
D:(0,0,0) ; A:(a,0,0) [où a=largeur du rectangle] ; C:(0,c,0) [où c=longueur du rectangle] ; B:(a,c,0) et S:(x,y,z)
Tes 3 infos concernant les distances donnent 3 équation concernant les 5 réels a,c,x,y,z et il faut ensuite regarder si, avec ça, tu arrive à en déduire la valeur de la longueur SD (avec 3 équations et 5 inconnues, c'est pas gagné, mais c'est pas impossible...)
Ca me semble un peu bizarre qu'on puisse conclure avec aussi peu d'information (tu as rien d'autre ?)
Si on prend un repère centré en D et dont les eux premier axes sont les droites (DA) et (DC) alors
D:(0,0,0) ; A:(a,0,0) [où a=largeur du rectangle] ; C:(0,c,0) [où c=longueur du rectangle] ; B:(a,c,0) et S:(x,y,z)
Tes 3 infos concernant les distances donnent 3 équation concernant les 5 réels a,c,x,y,z et il faut ensuite regarder si, avec ça, tu arrive à en déduire la valeur de la longueur SD (avec 3 équations et 5 inconnues, c'est pas gagné, mais c'est pas impossible...)
Modifié en dernier par Ben314 le 30 Sep 2018, 18:58, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Problème maths pyramide
Merci Ben314 pour ton aide ! Je vais essayé de me débrouiller avec ce que tu m'as dit !
Re: Problème maths pyramide
En fait (et étonnement), ça marche et on peut même prouver de façon plus générale que dans une pyramide à base rectangulaire SABCD, on a systématiquement SA²+SC²=SB²+SD².
Et il doit sûrement y a avoir un moyen bien plus simple (i.e. sans passes par le système d'équation qui se simplifie miraculeusement) de prouver ce résultat.
Et il doit sûrement y a avoir un moyen bien plus simple (i.e. sans passes par le système d'équation qui se simplifie miraculeusement) de prouver ce résultat.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Problème maths pyramide
Ben justement, je vois pas bien comment tu l'utilise ici sans introduire les dimensions du rectangle qui vont "miraculeusement" disparaître à la fin.jlb a écrit:Théorème de Pythagore!
Tu peut détailler ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Problème maths pyramide
Effectivement, je ne comprends pas comment c'est possible d'utiliser Pythagore.
Re: Problème maths pyramide
Oui et non : je pense (enfin... j'espère) que tu as écrit que, avec les notations de mon post précédent (*) on aMa1817 a écrit:Effectivement, je ne comprends pas comment c'est possible d'utiliser Pythagore.
Et en fait, cette "formule" pour calculer la distance d'un point à un autre de l'espace de dimension 3, c'est la formule de Pythagore un peu "revisitée".
Ma question (à JLB), c'était de savoir s'il avait un moyen plus simple que celui là, (en particulier ne faisant éventuellement pas intervenir les dimensions du rectangle) pour répondre au problème.
Sinon, concernant la méthode (pas jolie) qui marche, tu écrit les 2 autres équations données par l'énoncé, puis évidement tu les élève au carré (pour virer les racines) puis tu doit constater qu'en les ajoutant/soustrayant de façon astucieuse, tu va en déduire la valeur de
(*) Attention, j'ai changé d'avis en cours de route et j'ai pris finalement D comme centre du repère.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Problème maths pyramide
Vous faites quel chapitre ?
Produit scalaire dans l'espace potentiellement... ?
Produit scalaire dans l'espace potentiellement... ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Problème maths pyramide
Soit H le plan perpendiculaire à (BC), perpendiculaire à ABCD et passant par S.
si on projette SBC sur sur plan et SAD sur ce plan, on a le résultat en 2 lignes. Pour expliquer pourquoi les projections marchent, il faut bcp d’explications.
si on projette SBC sur sur plan et SAD sur ce plan, on a le résultat en 2 lignes. Pour expliquer pourquoi les projections marchent, il faut bcp d’explications.
Re: Problème maths pyramide
Lostounet a écrit:Vous faites quel chapitre ?
Produit scalaire dans l'espace potentiellement... ?
Nous faisons les fonctions ! Ce qui n'a absolument rien avoir !
Re: Problème maths pyramide
Sauf erreur, tu projettes le sommet S de la pyramide en point H sur le plan contenant la base rectangulaire et tu obtiens avec th de Pythagore SA²+SC²= 2SH²+HA²+HC², idem pour SB²+SD² et tu réécris HA²,HB²,HC²,HD² avec le th de Pythagore en utilisant les projections de H sur les support des cotés du rectangle. Et hop, c'est magique! 

Modifié en dernier par jlb le 30 Sep 2018, 21:01, modifié 2 fois.
Re: Problème maths pyramide
Ma1817 a écrit:Je n'ai pas trop compris la formule "revisitée"
Bon il va falloir nous dire tu es en quelle classe, et ce que tu connais comme outils...
Tu as fait l'année dernière le chapitre de géométrie dans l'espace? Le produit scalaire?
La formule de Pythagore dans un repère de l'espace?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Problème maths pyramide
Lostounet a répondu en même temps que moi, je ne sais pas si vous avez "rencontré ma réponse"! Voir au dessus. En gros, c'est la même démarche mais sans système ni coordonnées.
Re: Problème maths pyramide
En fait, il n'y aucun calcul à faire, ou presque.
Le carré du trajet d'un coin de la base jusqu'au sommet est égal à la somme des carrés des trajets qui suivent les axes Ox, Oy et Oz. En comparant le trajet ASC avec BSD, l'égalité qui a été relevée est immédiate.
Le carré du trajet d'un coin de la base jusqu'au sommet est égal à la somme des carrés des trajets qui suivent les axes Ox, Oy et Oz. En comparant le trajet ASC avec BSD, l'égalité qui a été relevée est immédiate.
Re: Problème maths pyramide
Sinon, pour une preuve ne faisant (quasiment) pas intervenir les dimensions du rectangle (ni la dimension de l'espace), par simple développement des carrés (scalaires), on a :
 où
où  est le milieu de
est le milieu de 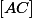
Et comme est aussi le milieu de
est aussi le milieu de 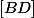 et que
et que  on conclue bien que
on conclue bien que  .
.
Et cela montre en fait que, pour 4 points A,B,C,D d'un espace euclidien E de dimension quelconques, il y a équivalence entre le fait que ABCD soit un rectangle et le fait que,pour tout S de E on ait SA²+SC²=SB²+SD².
Et comme
Et cela montre en fait que, pour 4 points A,B,C,D d'un espace euclidien E de dimension quelconques, il y a équivalence entre le fait que ABCD soit un rectangle et le fait que,pour tout S de E on ait SA²+SC²=SB²+SD².
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
