Polynômes - fractions rationnelles

[leusca]

Bonjour à tous,
Voici le problème:
Considérons le polynôme

P(x)= x^4-2x^3-x^2-2x+1

Demontrez que si xo est une racine de P alors 1/xo est aussi racine de P.

Ce que j'en pense:
Si j'ai bien compris ce polynôme n'a pas de racine "évidente" (1 ; 0 ; -1) comme il l'explique dans le cour. L'énoncé considère donc xo comme racine. Je peux sans problème écrire:

P(xo)= xo^4 - 2xo^3 - xo^2 - 2xo +1 = 0

et toujours d'après l'enoncé:

P(1/xo)= 1/xo^4 - 2/xo^3 - 1/xo^2 - 2/xo +1 = 0

On me demande de démontrer que P(xo)= 0 = P(1/xo) ou

xo^4 - 2xo^3 - xo^2 - 2xo +1 = 0 = 1/xo^4 - 2/xo^3 - 1/xo^2 - 2/xo +1

Apartir de là je me suis rendu compte qu'il y'avait un truc qui allait pas. et la solution de l'exercice ne m'aide pas du tout a comprendre.

Merci d'exposer une réponse claire.

[oscar]

C' est une équation SYMETRIQUE

P(x) =X^4 -2x³ - x² -2x + 1=0

Diviser tuous les termes par x²

P(x) = x² -2x -1 -2/ x +1/x²=0
..Grouper les termes

P(x) = ( x² +1/x²) -2 ( x +1/x) - 1=0 (1)

POser( x+1/x = y => x²+1/x² =(x²+ 2 +y²) = ( x+y)² -2

(1) devient y² -2 -2y -1=0 <=> y² -2y -3=0
Détermine y puis x

[Dinozzo13]

Salut !

, par conséquent si est racine de alors .
Si est racine de alors .
Calcule alors et réduis tout sous le même dénominateur.
Pour montrer que , il te suffit donc de montrer que le numérateur du quotient obtenu est nul.
Pour cela tu l'écris en fontion de .
Ensuite pose pour tout réel non nul :

Montre que pour tout non nul, .
Puis exprime en fonction de .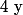
Résous l'équation du second degré d'inconnue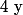 obtenue.
Déduis-en les solutions de l'équation .

En espérant t'avoir aidé :++: