Points coplanaires
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Lory
- Membre Naturel
- Messages: 23
- Enregistré le: 22 Aoû 2005, 09:58
-
 par Lory » 31 Oct 2005, 13:23
par Lory » 31 Oct 2005, 13:23
Pouvez-vous m'aider sur la question suivante, voici l'énoncé ( faire une figure ) :
ABCDE est une pyramide de sommet A et de base le parallélogramme BCDE.
I est le centre de BCDE. J est le centre de gravité du triangle ACD.
K est le milieu du segment [BE]. L est le point tel que (vecteur) AL= 4/5 AI (vecteur).
M est le milieu de [CD].
1) démontrer que les points A,K,M,I,J,L sont coplanaires.
merci
SVPPP aidez-moi!!!
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 31 Oct 2005, 13:45
par becirj » 31 Oct 2005, 13:45
Bonjour
Parmi les 6 points, il faut considérer une base de 2 vecteurs non colinéaires , je te conseille de prendre les vecteurs

et
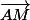
et exprimer les vecteurs

dans la base choisie c'est-à-dire en fonction des 2 vecteurs choisis (ou d'un seul).
-
Lory
- Membre Naturel
- Messages: 23
- Enregistré le: 22 Aoû 2005, 09:58
-
 par Lory » 31 Oct 2005, 14:00
par Lory » 31 Oct 2005, 14:00
Il faut que je fasse des combinaisons linéaires alors ?
J'ai pas trés bien compris.
D'aprés ce que tu as di j' ai écrit :
AL=4/5AI
AJ= 2/3AM
Mais je pense que ce n'est pas ca!
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 31 Oct 2005, 14:14
par becirj » 31 Oct 2005, 14:14
Il faut encore que tu exprimes
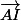
en fonction de

et
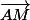
. IL faut effectivement avoir des combinaisons linéaires de

et
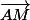
.
-
Lory
- Membre Naturel
- Messages: 23
- Enregistré le: 22 Aoû 2005, 09:58
-
 par Lory » 31 Oct 2005, 14:23
par Lory » 31 Oct 2005, 14:23
je n'arrive pas à trouver la combinaison avec le vecteur AI c'est impossible!!
j'arrive seulement à écrire (en vecteur) AI= 2/3 AM + JI
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 31 Oct 2005, 14:29
par becirj » 31 Oct 2005, 14:29
Cette combinaison ne donne rien.
I étant le centre du parallélogramme est le milieu de [KM]. Tu peux le montrer en utilisant des égalités vectorielles.
Montrer ensuite que
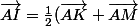)
-
Lory
- Membre Naturel
- Messages: 23
- Enregistré le: 22 Aoû 2005, 09:58
-
 par Lory » 31 Oct 2005, 14:40
par Lory » 31 Oct 2005, 14:40
désolé mais je ne comprend pas comment tu as fait pour trouver AI= 1/2 (AK+AM) ??
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 31 Oct 2005, 14:50
par becirj » 31 Oct 2005, 14:50


En additionnant membre à membre les deux égalités et en remarquant que

puisque I est le milieu de [KM], on arrive à l'égalité cherchée.
-
Lory
- Membre Naturel
- Messages: 23
- Enregistré le: 22 Aoû 2005, 09:58
-
 par Lory » 31 Oct 2005, 15:03
par Lory » 31 Oct 2005, 15:03
Ahhhh oui d'accord fallait le trouver quand meme!! :hum: merci beaucoup
donc si je résume tout :
AI = 1/2 (AK+AM) donc AI, AK, AM sont coplanaires donc les points A,K,M,I,J,L sont coplanaires
c'est correct?
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 31 Oct 2005, 15:32
par becirj » 31 Oct 2005, 15:32
Il faudrait quand même que tu écrives

en fonction de

et
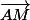
ce qui est facile puisque tu as

en fonction de
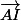
-
Lory
- Membre Naturel
- Messages: 23
- Enregistré le: 22 Aoû 2005, 09:58
-
 par Lory » 31 Oct 2005, 15:42
par Lory » 31 Oct 2005, 15:42
Ah oui je l'avais oublié !
donc AL = 2/5 (AK+AM)
et est-ce qui faut aussi que j'écrive le vecteur AJ en fonction de AK et AM ?
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 31 Oct 2005, 16:54
par becirj » 31 Oct 2005, 16:54
Tu l'as uniquement en fonction de
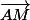
mais cela suffit.
-
Lory
- Membre Naturel
- Messages: 23
- Enregistré le: 22 Aoû 2005, 09:58
-
 par Lory » 31 Oct 2005, 17:07
par Lory » 31 Oct 2005, 17:07
Merci Beaucoup Pour Toute Ton Aide :++:
@+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
