BONSOIR! Besoin d'aide! Determiner une partie génératrice du s.e.v suivant
F= {(x,y,z) € R^3 , x+y+z=0 ; x=2y} Je fais bien avec la premiere equation sa me donne cette partie generatrice {(1,0,1) ; (0,1,1)} mais je me demande à quoi sert la deuxieme equation x=2y?
PARTIE GENERATRICE ESPACE VECTORIEL
8 messages
- Page 1 sur 1
Re: PARTIE GENERATRICE ESPACE VECTORIEL
Salut déjà la famille génératrice que tu donnes ne convient pas avec F en effet 1+0+1 est différent de 0 (de même pour l'autre vecteur) ...
La première chose à faire quand on te demande trouver une famille génératrice et que tu as plusieurs équations et plusieurs variables c'est d'exprimer le plus de variable en fonction d'une seule si c'est possible.
En effet la on te donne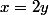 et avec
et avec 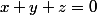 tu en déduis que
tu en déduis que 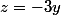
Donc si le triplet\in F) <=>
<=>=(2y,y,-3y)) <=>
<=> =y(2,1,-3))
Donc tu en déduis une famille génératrice de F.
La première chose à faire quand on te demande trouver une famille génératrice et que tu as plusieurs équations et plusieurs variables c'est d'exprimer le plus de variable en fonction d'une seule si c'est possible.
En effet la on te donne
Donc si le triplet
Donc tu en déduis une famille génératrice de F.
Re: PARTIE GENERATRICE ESPACE VECTORIEL
bsr,

une famille génératrice est constituée du vecteur de coordonnées)
une famille génératrice est constituée du vecteur de coordonnées
Re: PARTIE GENERATRICE ESPACE VECTORIEL
Bonsoir,
Tu as pu remarquer que F est l'intersection de 2 plans vectoriels. On obtient une droite vectorielle. Une partie génératrice de la droite peut être constituée d'un seul vecteur non nul de la droite.
Tu as pu remarquer que F est l'intersection de 2 plans vectoriels. On obtient une droite vectorielle. Une partie génératrice de la droite peut être constituée d'un seul vecteur non nul de la droite.
Re: PARTIE GENERATRICE ESPACE VECTORIEL
Et si je veux trouver une partie generatrice de ce s.e.v comment est-ce-que je procede?
E={(x;x+y;-x+2y) ; x,y € R}
E={(x;x+y;-x+2y) ; x,y € R}
Re: PARTIE GENERATRICE ESPACE VECTORIEL
Il faut trouver un système paramétrique des vecteurs de E, de paramètres x et y.
M appartient à E ssi M = x * u + y * v, les vecteurs u et v sont à trouver.
M appartient à E ssi M = x * u + y * v, les vecteurs u et v sont à trouver.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 229 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
