Parabole, droite et rectangle.

par **Deluxor** » 28 Déc 2009, 13:09

Bonjour à tous,

Voici un exercice que j'ai à cherché et dont je n'arrive pas à bout. Je n'ai vraiment aucune piste de départ.

L'énoncé est le suivant :

h est un réel strictement positif.

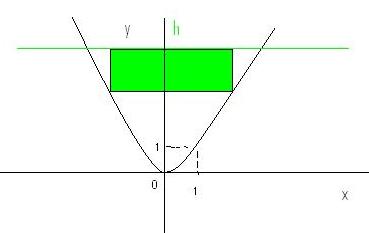
Dans la portion du plan, muni d'un repère orthonormal déterminé par l'arc de parabole d'équation y=x² et la droite d'équation y=h, on veut inscrire, comme sur la figure ci-contre un rectangle dont l'aire soit la plus grande possible.

Prouvez qu'un tel rectangle existe ; donnez ses dimensions en fonctions de h.

Merci à tous.

par **Anonyme** » 28 Déc 2009, 13:27

Considere M(x,y) un sommet du rectangle.
Commence par calculer en fonction de x et de h la largeur et la longueur du rectangle.
Encadre x.

Commence par faire cela avant de continuer.

par **Deluxor** » 28 Déc 2009, 13:33

D'accord, alors si je considère un point M(x;y) sommet du rectangle.

La largeur du rectangle vaut h-y.

Et la longueur vaut 2x.

Non ?

par **Anonyme** » 28 Déc 2009, 13:40

Tu as pris M dans le premier cadran. (fais attention x est positif pour la suite du probleme)

Dans ce cas en effet
longueur = 2x
et la largeur = h-y
or y vaut quoi ?

et puis pense a encadrer x :
On a choisi x >0 il reste a calculer sa valeur maximale pour pouvoir l'encadrer.

Ensuite tu pose a(x)= aire du rectangle en fonction de x

C'est bon jusque la ?

par **Deluxor** » 28 Déc 2009, 13:43

y = x²

Donc : longueur = 2x et largeur = h-x²

Valeur maximale de x ? Il n'y en n'a pas de fixée, si ?

par **Ericovitchi** » 28 Déc 2009, 13:49

Il te faut étudier la fonction 2x(h-x²) et regarder si elle a un maximum avant de dire qu'il n'y en pas pas de fixé !

(Ca n'est pas la valeur maximum de x que l'on cherche c'est la valeur maximum de l'aire)

par **Anonyme** » 28 Déc 2009, 13:58

Il faut calculer la valeur maximale de x pour pouvoir trouver dans quel intervalle varie x pour pouvoir juger si la valeur qu'on obtient a la fin est acceptable ou inacceptable.

Graphiquement tu remarque que la valeur maximale de x est atteinte quand
y=h
donc x^2=h
tu résous tu trouve deux valeurs de x dont seul une est acceptable (rappelle toi que x >0)

Ensuite comme l'a dis Ericovitchi tu etudie la fonction a(x) qui donne l'aire du rectangle en fonction de . a(x)=2x(h-x²)
Pour cela tu dois calculer la derivee puis faire le tableau de variation de la fonction. Dans le tableau tu trouvera la maximum de a(x) et pour quelle valeur de x celui ci est atteint.
Il te reste a la fin de verifier si cette valeur de x est contenu dans l'intervalle qu'on a calcule precedemment et de conclure.

Bonne chance :++:
(J'ai mis tout d'un coup car il faut que je parte)

par **Deluxor** » 28 Déc 2009, 14:07

D'accord, j'ai compris.

Donc :

- pour "prouver qu'un tel rectangle existe" il faut que je prouve qu'une valeur de x est acceptable ? Par contre je ne comprends pas comment on peut dire que la valeur maximale de x est atteinte quand y = h ?

par **Ericovitchi** » 28 Déc 2009, 14:12

En regardant le dessin, on voit bien que pour que le rectangle existe, il faut que x n'ait pas dépassé le point d'intersection entre la parabole et la droite y=h

par **Deluxor** » 28 Déc 2009, 14:16

On en déduit que : 0 < x < Vh ?

par **Ericovitchi** » 28 Déc 2009, 14:19

Oui. Et maintenant pour regarder le x qui donne la plus grande aire possible, il te faut étudier la fonction 2x(h-x²) pour x variant dans cet intervalle

par **Deluxor** » 28 Déc 2009, 14:28

D'accord.

Alors j'ai trouvé la dérivée. Mais j'ai toujours un problème dans la rédaction ...

On cherche à étudier une fonction sur un intervalle précis. On doit tout de même d'abord établir le tableau de variation de la fonction sur R, non ?

par **Ericovitchi** » 28 Déc 2009, 14:40

oui qu'est-ce qui t'empêche de faire le tableau de variation ?

Parabole, droite et rectangle.

Parabole, droite et rectangle.

Qui est en ligne