Logarithme...Kézaco ?

[pives]

J’ai une question qui peut paraitre bête pour certains, mai la réponse sera d’autant plus rapide pour d’autre :

En clair c’est quoi un logarithme :doh:

Cette notion ne me parle pas du tout, alors si quelqu’un m’aider…

Merci d’avance.

[lapras]

Salut,
en quelle classe es tu ?
As tu vu les dérivées ?

[Benjamin]

Bonjour,

Le logarithme népérien est une fonction. Au même titre que f(x) = x² en est une. On la note ln. En fait, cette fonction est la réciproque de la fonction exponentielle. C'est-à-dire que ln(exp(x))=x. Ainsi, elle présente des propriétés duales à la fonction exponentielle :
ln(a*b)=ln(a)+ln(b) (dual de exp(a+b)=exp(a)*exp(b))
ln(x^n)=n*ln(x) (dual de (exp(x))^n=exp(n*x))

[pives]

Je suis plus au lycée depuis quelques années déjà ... Je me pose la question par curiosité (j’ai aborder la notion en cherchant des infos sur le pH, avec des log de H+ et tout le tralala…).
J’étais pas très bon en maths, mais les fonctions çà me parle un peu quand même… par contre les dérivées trou noir total !!

[pives]

Rien à voir, mais l'horloge du forum à une heure de retard...

Je médite sur ta réponse Benjamin 631....

[pives]

Ok, merci pour les réponses...

J'ai quand même une autre question.Je me suis penché sur le pH de l'eau, et je suis tombé la dessus:

pH = ;)log10 [H3O+]

Je comprend pas le "-log"... :briques:

[Benjamin]

Déjà, le forum n'a pas de problème d'horloge. Il faut que tu règles les options dans ton profil pour te mettre en GMT+2.
Ensuite, le log10, c'est pas la même chose que ln.

De même que le logarithme népérien est la réciproque de l'exponentiel, le logarithme en base 10 est la réciproque de la fonction f(x)=10^x.
log10(10^x)=x.

Quant à ph=-log[H3O+], c'est tout simplement la définition du pH, on n'y peut pas grand chose.

[Dominique Lefebvre]

Ok, merci pour les réponses...

J'ai quand même une autre question.Je me suis penché sur le pH de l'eau, et je suis tombé la dessus:

pH = log10 [H3O+]

Je comprend pas le "-log"... :briques:

Bonjour,
Le log décimal d'un nombre plus petit que 1 est un nombre négatif. [H30+] est plus petit que 1. Par convention, le pH est un nombre positif. On multiplie le log par -1 pour que le résultat soit positif...

PS : c'est du moins l'explication la plus simple...

[pives]

Benjamin 631 à dit:

"De même que le logarithme népérien est la réciproque de l'exponentiel, le logarithme en base 10 est la réciproque de la fonction f(x)=10^x"

Excuses-moi de ne pas avoir précisé plus tôt....

Merci pour vos réponses, j'ai de quoi avancer un peu plus.

A+

[Benjamin]

C'est plus ou moins la même chose en fait. En effet, si tu prends un réel strictement positif a, tu as : 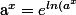(car pour tout réel x, je te rappelle que ) et donc 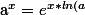. Ainsi, la fonction puissance, c'est une fonction exponentielle particulière.

De , on a .

On définit alors le logarithme en base a comme étant : . Toute les propriétés de la fonction logarithme népérien se retrouve donc dans le logarithme en base a. En fait, .

[pives]

.

J'ai pas tous compris au développement, mais cette conclusion me plait pas mal... :ptdr: