Bonjour,
Je cherche des cours pour comprendre ce que signifie Log2 et Log10. Il me semblait que je pouvais trouver ce genre de choses dans les programmes de lycée mais jusqu'ici je ne vois pas. J'en ai besoin pour préparer des révisions de concours.
Louis.
Log2 et Log10
12 messages
- Page 1 sur 1
Re: Log2 et Log10
https://www.maths-france.fr/Terminale/T ... perien.pdf
Regarde tout à la fin pour le logarithme décimal = logarithme en base 10 = Log10 (IV.)
Pour le logarithme en base 2, c'est pareil en remplaçant 10 par 2
Regarde tout à la fin pour le logarithme décimal = logarithme en base 10 = Log10 (IV.)
Pour le logarithme en base 2, c'est pareil en remplaçant 10 par 2
Re: Log2 et Log10
Très grossièrement le log en base 10 est le nombre de chiffres (en base 10) nécessaire pour écrire le nombre.
Ainsi si log10(x) = 7.43 tu sais que 10^7 < x < 10^8
Idem en base 2 en remplacçant 10 par 2
Ainsi si log10(x) = 7.43 tu sais que 10^7 < x < 10^8
Idem en base 2 en remplacçant 10 par 2

Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Log2 et Log10
Merci Sylviel c'est une bonne première indication 
Les questions types auxquelles je dois savoir répondre pour mon concours doivent paraître toutes simples pour des personnes s'y connaissant mais requiert pour moi d'étudier des chapitres entier seul.
Auriez vous des indications à me donner ? Elles ressemblent à ça :
Si log2 (x+2) = 5 alors x = 30 : Vrai ou Faux ?
Si log10 ((x+1)(x-1)) = 3log102 alors x = 3 : Vrai ou Faux ?

Les questions types auxquelles je dois savoir répondre pour mon concours doivent paraître toutes simples pour des personnes s'y connaissant mais requiert pour moi d'étudier des chapitres entier seul.
Auriez vous des indications à me donner ? Elles ressemblent à ça :
Si log2 (x+2) = 5 alors x = 30 : Vrai ou Faux ?
Si log10 ((x+1)(x-1)) = 3log102 alors x = 3 : Vrai ou Faux ?
Re: Log2 et Log10
Il faut comprendre que x-> log2(x) est la fonction réciproque de x-> 2^x,
tout comme x->log10(x) est la fonction réciproque de x ->10^x, ou comme x->ln(x) est la fonction réciproque de x-> e^x.
Donc pour résoudre l'équation log2(x+2)=5, on peut faire :
log2(x+2)=5 ssi x+2=2^5 (j'ai appliqué x->2^x à chaque membre).
De même avec les log10 :
log10((x+1)(x-1))=3log10(2)=log10(8) ssi (x+1)(x-1) = 8 (j'ai appliqué x -> 10^x à chaque membre).
tout comme x->log10(x) est la fonction réciproque de x ->10^x, ou comme x->ln(x) est la fonction réciproque de x-> e^x.
Donc pour résoudre l'équation log2(x+2)=5, on peut faire :
log2(x+2)=5 ssi x+2=2^5 (j'ai appliqué x->2^x à chaque membre).
De même avec les log10 :
log10((x+1)(x-1))=3log10(2)=log10(8) ssi (x+1)(x-1) = 8 (j'ai appliqué x -> 10^x à chaque membre).
Re: Log2 et Log10
Bonjour ;
Prenons tout d'abord qui est le logarithme de base
qui est le logarithme de base  .
.
On remarque ici qu'on parle de base , c-à-d que tout nombre réel
, c-à-d que tout nombre réel  strictement
strictement
positif , peut s'écrire sous la forme d'une puissance de ; c-à-d il existe un nombre réel
; c-à-d il existe un nombre réel  tel
tel
que : .
.
On appelle ce " " :
" : ) .
.
Exemples :
On a :
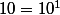 ; donc
; donc  = 1) .
.
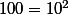 ; donc
; donc  = 2) .
.
 ; donc
; donc  \approx 1,80618) .
.
Maintenant prenons qui est le logarithme de base
qui est le logarithme de base  .
.
Donc tout nombre réel strictement positif , peut s'écrire sous la forme
strictement positif , peut s'écrire sous la forme
d'une puissance de ; c-à-d il existe un nombre réel
; c-à-d il existe un nombre réel  tel que :
tel que :  .
.
On appelle ce " " :
" : ) .
.
Exemples :
On a :
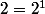 ; donc
; donc  = 1) .
.
 ; donc
; donc  = 2) .
.
 ; donc
; donc  \approx 3,3215) .
.
Tu peux prendre n'importe quelle base pour le logarithme , il suffit qu'elle soit
strictement positive .
Prenons tout d'abord
On remarque ici qu'on parle de base
positif , peut s'écrire sous la forme d'une puissance de
que :
On appelle ce "
Exemples :
On a :
Maintenant prenons
Donc tout nombre réel
d'une puissance de
On appelle ce "
Exemples :
On a :
Tu peux prendre n'importe quelle base pour le logarithme , il suffit qu'elle soit
strictement positive .
Re: Log2 et Log10
LB2 a écrit:Il faut comprendre que x-> log2(x) est la fonction réciproque de x-> 2^x,
tout comme x->log10(x) est la fonction réciproque de x ->10^x, ou comme x->ln(x) est la fonction réciproque de x-> e^x.
Donc pour résoudre l'équation log2(x+2)=5, on peut faire :
log2(x+2)=5 ssi x+2=2^5 (j'ai appliqué x->2^x à chaque membre).
De même avec les log10 :
log10((x+1)(x-1))=3log10(2)=log10(8) ssi (x+1)(x-1) = 8 (j'ai appliqué x -> 10^x à chaque membre).
Donc si je comprend bien pour la première équation je me retrouve avec : x + 2 = 32 --> x = 30, c'est donc Vrai
Et pour la deuxième (x+1)(x-1) = 8 donc l'équation est bien égale à 3log10(2), c'est donc Vrai
?
Re: Log2 et Log10
aymanemaysae a écrit:Bonjour ;
Prenons tout d'abordqui est le logarithme de base
.
On remarque ici qu'on parle de base, c-à-d que tout nombre réel
strictement
positif , peut s'écrire sous la forme d'une puissance de; c-à-d il existe un nombre réel
tel
que :.
On appelle ce "" :
.
Exemples :
On a :; donc
.
; donc
.
; donc
.
Maintenant prenonsqui est le logarithme de base
.
Donc tout nombre réelstrictement positif , peut s'écrire sous la forme
d'une puissance de; c-à-d il existe un nombre réel
tel que :
.
On appelle ce "" :
.
Exemples :
On a :; donc
.
; donc
.
; donc
.
Tu peux prendre n'importe quelle base pour le logarithme , il suffit qu'elle soit
strictement positive .
Merci beaucoup pour cette explication, je comprend mieux le fonctionnement des Log !
Re: Log2 et Log10
LouisDS a écrit:LB2 a écrit:Il faut comprendre que x-> log2(x) est la fonction réciproque de x-> 2^x,
tout comme x->log10(x) est la fonction réciproque de x ->10^x, ou comme x->ln(x) est la fonction réciproque de x-> e^x.
Donc pour résoudre l'équation log2(x+2)=5, on peut faire :
log2(x+2)=5 ssi x+2=2^5 (j'ai appliqué x->2^x à chaque membre).
De même avec les log10 :
log10((x+1)(x-1))=3log10(2)=log10(8) ssi (x+1)(x-1) = 8 (j'ai appliqué x -> 10^x à chaque membre).
Donc si je comprend bien pour la première équation je me retrouve avec : x + 2 = 32 --> x = 30, c'est donc Vrai
Et pour la deuxième (x+1)(x-1) = 8 donc l'équation est bien égale à 3log10(2), c'est donc Vrai
?
Ok pour la première. Vrai.
Attention à la logique pour la deuxième. x=3 est solution mais il y a aussi x = -3. Donc c'est Faux.
Re: Log2 et Log10
@LB2 Ah ! Très bien, c'est un piège pour me faire croire que la réponse est vraie alors qu'il manque une partie de la solution.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
