Bonjour j'ai besoin d'aide pour trouver la limite de cette suite. J'ai trouvé qu'il s'agissait d'une forme indéterminée car -2n tend vers - l'infini alors que racine de n tend vers + l'infini. Je sais qu'il faudrait factoriser mais je ne sais pas par quoi.
Un = √n - 2n
http://hpics.li/bf252d9
Limite d'une suite
11 messages
- Page 1 sur 1
Re: Limite d'une suite
DiamondF a écrit:On factorise par n et on fait Un = n((1/ √n)-2) ?
Salut, oui tout à fait: on prend en facteur le terme le plus puissant (ici n) (puissant au sens puissance la plus élevée !). Cela lève l'indétermination.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Limite d'une suite
D'accord merci, j'ai trouvé : Un = n((1/ √n)-2)
avec n→ + l'infini
avec 1/ √n → 0
avec -2 → -2
Par somme limite de 1/√n - 2 → -2
et par produit Un → - l'infini (car -2 est négatif n strict.positif)
Merci de votre aide, en fait ce qui me gêner c'était de factoriser √n par n car j'avais oublié, sur mon cahier d'exercices c'est mieux rédiger mais là, je n'arrive pas à insérer les formules j'espère que vous me comprenez.
avec n→ + l'infini
avec 1/ √n → 0
avec -2 → -2
Par somme limite de 1/√n - 2 → -2
et par produit Un → - l'infini (car -2 est négatif n strict.positif)
Merci de votre aide, en fait ce qui me gêner c'était de factoriser √n par n car j'avais oublié, sur mon cahier d'exercices c'est mieux rédiger mais là, je n'arrive pas à insérer les formules j'espère que vous me comprenez.
Re: Limite d'une suite
Merci de ton aide ! Concernant la méthode que tu me proposes je l'ai comprise, j'en prends note, elle me parait plus simple, il vaut mieux 2 méthodes plutôt qu'une!
Re: Limite d'une suite
DiamondF a écrit:Merci de ton aide ! Concernant la méthode que tu me proposes je l'ai comprise, j'en prends note, elle me parait plus simple, il vaut mieux 2 méthodes plutôt qu'une!
Re,
Excuses je me suis trompé..J'avais pas la tête en place!
(n) ne tend pas vers -infini attention.
Mais on peut corriger l'étourderie.
On peut constater que Un < -n + 1
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Limite d'une suite
DiamondF a écrit:Ce n'est pas grave! Je l'avais corrigé, merci de votre aide, bonne soirée
En fait si tu veux bien justifier la seconde méthode (pas facile mais accroche toi!)
Considérons le polynôme X^2-X+1. Il atteint son minimum en x=-b/2a=1/2 et vaut 3/4.
On a donc que X^2-X+1> 0
Prends maintenant X=racine(n)
donc X^2=n
alors on conclut que n - racine(n) +1>0
donc racine(n)< n+1
racine(n)-2n < - n + 1
Un < -n+1
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Limite d'une suite
J'ai suivi étape par étape, et je pense avoir compris, j'ai repris ta méthode car elle est intéressante
Pour le minimum t'as fait X=-(-1)/2*1= 1/2 et si on fait la f(x) on obtient 3/4
Donc X^2-X+1> 0 , Quand X= racine(n) on a la racine qui s'enlève pour le X^2 = n
Soit n - racine(n) +1>0 car X^2-X+1> 0
Après t'as fait racine(n) < n + 1
- On ajoute -2n
Soit racine(n) -2n < - n + 1
Un < -n+1
Pour le minimum t'as fait X=-(-1)/2*1= 1/2 et si on fait la f(x) on obtient 3/4
Donc X^2-X+1> 0 , Quand X= racine(n) on a la racine qui s'enlève pour le X^2 = n
Soit n - racine(n) +1>0 car X^2-X+1> 0
Après t'as fait racine(n) < n + 1
- On ajoute -2n
Soit racine(n) -2n < - n + 1
Un < -n+1
Re: Limite d'une suite
Tu as tout compris!
Bravo pour ton sérieux. N'hésite pas à revenir si tu as des questions
Bravo pour ton sérieux. N'hésite pas à revenir si tu as des questions
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Limite d'une suite
salut
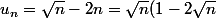) de la forme -oo * +oo
de la forme -oo * +oo

...
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
