Limite et trigonométrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 27 Fév 2007, 19:01
par MacErmite » 27 Fév 2007, 19:01
Bonsoir,
Je cherche à calculer la limite de cette chose :
)
lorsque x tend vers
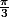
, elle est de forme indeterminée et je ne m'en sorts pas, pouvez-vous m'aider ?
la méthode m'interesse plus que de savoir si par exemple cela fait 1/2
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 19:16
par amine801 » 27 Fév 2007, 19:16
slt
on utilise le fait que
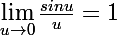
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 27 Fév 2007, 19:46
par MacErmite » 27 Fév 2007, 19:46
c'est un developpement limité avec sin u = u lorsque u tend vers 0 ?
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 19:54
par amine801 » 27 Fév 2007, 19:54
unitile de parle de DL(pas encore vu je suppose) juste la regle de l'hopital
mais normalment ctte formule doit etre dans vos formulaires.. :we:
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 27 Fév 2007, 19:57
par MacErmite » 27 Fév 2007, 19:57
La forme DL m'interesse mais je ne trouve pas la forme de ce DL ...
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 20:05
par amine801 » 27 Fév 2007, 20:05
je t'expose la methode pour faire la limite
on prend

}{1-2cos(x)).(x-\frac{\pi}{3}).\frac{sin(x-\frac{\pi}{3}}.{x-\frac{\pi}{3}}))
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 20:19
par amine801 » 27 Fév 2007, 20:19
je t'expose la methode pour faire la limite
on prend

}{1-2cos(x)}.(x-\frac{\pi}{3}).\frac{sin(x-\frac{\pi}{3})}{x-\frac{\pi}{3}})
}{1-2cos(x)}.(x-\frac{\pi}{3}))
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 27 Fév 2007, 20:20
par MacErmite » 27 Fév 2007, 20:20
En posant

d'ou
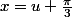
et donc en remplaçant x par u cela donne :
}{g(u)}=\frac{1}{2}\cdot \frac{sin(u)+\sqrt{3}.cos(u)}<br />{1-cos(u)+\sqrt{3}.sin(u)}\cdot sin(u))
en dérivant
}{g'(u)}=\frac{\sqrt{3}cos(2u)+sin(2u)}<br />{2\sqrt{3} cos(u)+2 sin(u)})
avec u=0 cela donne 1/2.
Merci pour ton aide. Comment as tu deviné que Hospital pouvait donner une solution viable ?
(nos messages ce sont croisés)
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 20:36
par amine801 » 27 Fév 2007, 20:36
c'est une fraction alors pourquoi pas :we:
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 27 Fév 2007, 21:08
par MacErmite » 27 Fév 2007, 21:08
je viens de me rendre compte que l'on pouvait trouver ce même résultat et toujours avec Hospital en utilisant directement la limite du début et donc sans le passage avec u... Il est fort ce principe lol
Par contre je ne trouve pas le DL :cry:
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 27 Fév 2007, 21:19
par amine801 » 27 Fév 2007, 21:19
si tu tient vraiment a voir un D.L utilise la formule de taylor
au voisinage de
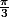
mais en général des qu'on travaille pas sur 0 le cest moins pratique
bon courage je suis pas un grand fan des calculs tu peux aussi faire un changement de variable combine a un DL en 0 mais avec cette méthode il est facile de faire des erreurs
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités