Limite par absurde

[moullmat6]

bonjours, sachant que la suite u(n) est convergente et vérifie: u(n)^n+ Arctan(u(n)) -1 =0 ; comment calculer sa limite par absurde .merci.

[Carpate]

bonjours, sachant que la suite u(n) est convergente et vérifie: u(n)^n+ Arctan(u(n)) -1 =0 ; comment calculer sa limite par absurde .merci.

Par l'absurde ? Je ne vois pas ,
Mais on peut déjà dire que doit être inférieur à

[Lostounet]

Je tente:
Soit L la limite de Un<+infini

comme |L|<=1 (sinon L^n va diverger, si Un tend vers 1, par continuité de arctan et x^n sur R:

1+Arctan(1)-1=0
Absurde

Si abs(x)<1,

Arctan(L) = 1
L=tan(1)>1? Donc absurde

Si carpate est d'accord?

[JaCQZz]

Par l'absurde ? Je ne vois pas ,
Mais on peut déjà dire que doit être inférieur à

Si, en supposant que : est sans limite car : :
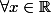
Or, l'égalité à démontrer dans l'énoncé est vérifiée pour tout . D'où : qui s'encadre n'est pas sans limites.

[Lostounet]

J'ai l'impression que si on travaille en degrés, il y a une limite mais si on travaille en rad non... pourquoi...ou c'est faux?

[JaCQZz]

Je tente:
Soit L la limite de Un1? Donc absurde

Si carpate est d'accord?

Oui et pour une conversion à l'identique au résultat, l'expression en rad ou degré, grad, n'y changera rien...
:
:

[nodjim]

@Lostounet: si u(n)=1+1/n, u(n)>1 mais u(n)^n ne diverge pas.

[nodjim]

u(n)^n ne diverge pas, je voulais dire.