Intégrer 1/sinx
24 messages
- Page 1 sur 2 - 1, 2
Intégrer 1/sinx
Tout est dans le titre !
Comment calcule t on l'intégrale de f:x -> 1/sin(x) ??
si vous avez ne serait-ce que des pistes, ça m'aiderait beaucoup
merci d'avance
Comment calcule t on l'intégrale de f:x -> 1/sin(x) ??
si vous avez ne serait-ce que des pistes, ça m'aiderait beaucoup
merci d'avance
...j'enfile ma cape...
sin2x=2cosx.sinx
1/sinx=2cosx/sin2x
je te laisse faire le reste, tu devrais y arriver maintenant
Sinon je reste près d'une cabine téléphonique.
1/sinx=2cosx/sin2x
je te laisse faire le reste, tu devrais y arriver maintenant
Sinon je reste près d'une cabine téléphonique.
Merci !!
Merci Triderou, je vais essayer avec ça
Je ne comprends pas ce que tu veux dire Reav par changement de variable : je n'ai jamais fait de changement de variable pour calculer des primitives. M'enfin bon, je vais essayer de me pencher un peu plus dessus.... histoire de voir concrètement de quoi il s'agit ;)
Merci en tout cas !
En cas de détresse, je sifflerai trois fois ....
Je ne comprends pas ce que tu veux dire Reav par changement de variable : je n'ai jamais fait de changement de variable pour calculer des primitives. M'enfin bon, je vais essayer de me pencher un peu plus dessus.... histoire de voir concrètement de quoi il s'agit ;)
Merci en tout cas !
En cas de détresse, je sifflerai trois fois ....
en fait en faisant le changement de variable tu te ramène à une fonction fractionnelle de polynomes (dans ce cas-ci) dont tu dois calculer la primitive, et c'est pas très compliquer qd on connais la méthode. Si t'as jamais vu, laisse tomber y'a surement une autre méthode, essai celle de triderou par exemple. Mais si tu as des questions n'hésites pas :)
bonne continuation ! ++
bonne continuation ! ++
bonjour
pas d'accord avec triderou ni reav.
En posant t=cosx, dt=-dxsinx
Et Prim(1/sinx dx)= Prim(-1/t² dt)
n'est pas exact
1/sinx=2cosx/sin2x
ne mène pas à une forme u'/u...
voyons:
pour trouver une primitive d'une fraction rationnelle incluant des fonctions trigo (si les règles de Bioche ne donnent rien), le mieux est de poser:
t=tan(x/2) ; dt=1/2(1+t²)dx
cela ramène à intégrer une fraction rationnelle.
(ça peut parfois être long mais, en général, ça aboutit)
car
sin(x)=2t/(1+t²) et cos(x)=(1-t²)/(1+t²) et tan(x)=2t/(1-t²)
dans le cas présent:
int(1/sin(x),x)=int(2/(1+t²)*(1+t²)/(2t),t)=int(1/t,t)=ln|t|=ln(|tan(x/2)|)
voila qui est fait.
ps: ceci se fait en général en 1ère d'étude sup.
pas d'accord avec triderou ni reav.
En posant t=cosx, dt=-dxsinx
Et Prim(1/sinx dx)= Prim(-1/t² dt)
n'est pas exact
1/sinx=2cosx/sin2x
ne mène pas à une forme u'/u...
voyons:
pour trouver une primitive d'une fraction rationnelle incluant des fonctions trigo (si les règles de Bioche ne donnent rien), le mieux est de poser:
t=tan(x/2) ; dt=1/2(1+t²)dx
cela ramène à intégrer une fraction rationnelle.
(ça peut parfois être long mais, en général, ça aboutit)
car
sin(x)=2t/(1+t²) et cos(x)=(1-t²)/(1+t²) et tan(x)=2t/(1-t²)
dans le cas présent:
int(1/sin(x),x)=int(2/(1+t²)*(1+t²)/(2t),t)=int(1/t,t)=ln|t|=ln(|tan(x/2)|)
voila qui est fait.
ps: ceci se fait en général en 1ère d'étude sup.
Salut à vous,
Je ne vois absolument pas l'intérêt de la remarque de Triderou (qui selon moi a mis sa cape à l'envers, donc ),
),
en revanche le changement de variable t=cosx est très pertinent et découle naturellement des règles de Bioche :
le calcul est alors très simple, puisqu'on obtient

Et en dérivant le résutat obtenu, on tombe bien sur 1/sinx, ce qui prouve qu'il n'y a pas d'erreur.

Je ne vois absolument pas l'intérêt de la remarque de Triderou (qui selon moi a mis sa cape à l'envers, donc
en revanche le changement de variable t=cosx est très pertinent et découle naturellement des règles de Bioche :
le calcul est alors très simple, puisqu'on obtient
Et en dérivant le résutat obtenu, on tombe bien sur 1/sinx, ce qui prouve qu'il n'y a pas d'erreur.
Mayday, mayday !
que la forme indiquée par Triderou ne mène pas à u'/u, ça j'ai pu m'en apercevoir hier soir en tentant désespérément de la ramener à quelque chose de faisable. (cela dit et sans aucune ironie : merci quand même Triderou ! :) )
et là je me permets de jouer l'élève chiante qui pose plein de questions sans rien comprendre (il faut bien que quelqu'un s'y colle de temps à autre):
-> les règles de Bioche ? mais encore ? :D
-> non je n'ai jamais "primitivé" en utilisant un changement de variable, mais visiblement il va falloir que je m'y mette (je rentre en prépa, d'où l'affolement)
et c'est là que je commence à être vraiment crispante :
comment passe t'on, en posant t=cosx , à int(-1/(1-t²),dt)...
parce que moi bêtement, candidement, je me dis :
"oh ! mais 1/sinx est égal à -1/(1-cos²x) ? et comment donc ? je veux bien que sin²x = 1- cos²x, on peut s'arranger et négocier, mais là quand même vous y allez un peu fort"
voyez l'étendue du désastre.
"à l'impossible nul n'est tenu"
vous êtes donc autorisés à abandonner toute tentative d'instruction sur ma personne :D
12h33 : ce charmant exercice est proposé par un magazine distribué gracieusement en fin d'année aux terminales S de mon lycée, j'ai nommé "l'officiel de la taupe", censé préparer ces chères têtes blondes à l'entrée dans le supérieur... sage initiative, le problème étant qu'il ne propose quasiment aucune correction.... et après, ce sont les gentils forumeurs qui se payent le boulot :D
merci encore en tous cas !
et là je me permets de jouer l'élève chiante qui pose plein de questions sans rien comprendre (il faut bien que quelqu'un s'y colle de temps à autre):
-> les règles de Bioche ? mais encore ? :D
-> non je n'ai jamais "primitivé" en utilisant un changement de variable, mais visiblement il va falloir que je m'y mette (je rentre en prépa, d'où l'affolement)
et c'est là que je commence à être vraiment crispante :
comment passe t'on, en posant t=cosx , à int(-1/(1-t²),dt)...
parce que moi bêtement, candidement, je me dis :
"oh ! mais 1/sinx est égal à -1/(1-cos²x) ? et comment donc ? je veux bien que sin²x = 1- cos²x, on peut s'arranger et négocier, mais là quand même vous y allez un peu fort"
voyez l'étendue du désastre.
"à l'impossible nul n'est tenu"
vous êtes donc autorisés à abandonner toute tentative d'instruction sur ma personne :D
12h33 : ce charmant exercice est proposé par un magazine distribué gracieusement en fin d'année aux terminales S de mon lycée, j'ai nommé "l'officiel de la taupe", censé préparer ces chères têtes blondes à l'entrée dans le supérieur... sage initiative, le problème étant qu'il ne propose quasiment aucune correction.... et après, ce sont les gentils forumeurs qui se payent le boulot :D
merci encore en tous cas !
'Non inscrite' ne t'inquiète pas le changement de variable n'est pas au programme de terminale (du moins pas à ma connaissance) 
Les règles de Bioche permettent de faire des changements de variables lorsque la fonction à intégrer met en jeu des fonctions trigo telles que sin et cos par exemple. Si comme le dit '12h33' ces règles n'aboutissent à rien, on fait un autre changement de variable, le plus souvent, t=tan(x/2), et moi j'ai fait t=cosx.
En posant t=cosx, tu vas faire "sauter" la fonction trigo sin (dans ton exo), c'est le but !
Donc t=cosx, on dérive et on obtient dt=-dxsinx dx=-dt/sinx
Maintenant on remplace : (sans le symbole d'intégrale pour simplifier)
1/sinx, dx = (1/sinx)*(-1/sinx), dt = -1/(1-cos²x), dt = -1/(1-t²), dt
A noter je pense que "mélanger" les 'x' avec le 'dt' n'est pas très rigoureux au point de vue de l'écriture, attendons d'autre avis pour ca, mais c'est juste pour que t'essaies de voir, enfin j'espère que c'est à peu près clair
Voilà, maintenant tu as une fraction rationnelle à dériver, et si tu connais tes primitives usuelles ben tu le fais de suite comme l'a fait Alpha.
++
Voilà un site qui te donne quelques primitives usuelles :
http://www.mathprepa.com/ (Méthode de calcule intégrales)
Les règles de Bioche permettent de faire des changements de variables lorsque la fonction à intégrer met en jeu des fonctions trigo telles que sin et cos par exemple. Si comme le dit '12h33' ces règles n'aboutissent à rien, on fait un autre changement de variable, le plus souvent, t=tan(x/2), et moi j'ai fait t=cosx.
En posant t=cosx, tu vas faire "sauter" la fonction trigo sin (dans ton exo), c'est le but !
Donc t=cosx, on dérive et on obtient dt=-dxsinx dx=-dt/sinx
Maintenant on remplace : (sans le symbole d'intégrale pour simplifier)
1/sinx, dx = (1/sinx)*(-1/sinx), dt = -1/(1-cos²x), dt = -1/(1-t²), dt
A noter je pense que "mélanger" les 'x' avec le 'dt' n'est pas très rigoureux au point de vue de l'écriture, attendons d'autre avis pour ca, mais c'est juste pour que t'essaies de voir, enfin j'espère que c'est à peu près clair
Voilà, maintenant tu as une fraction rationnelle à dériver, et si tu connais tes primitives usuelles ben tu le fais de suite comme l'a fait Alpha.
++
Voilà un site qui te donne quelques primitives usuelles :
http://www.mathprepa.com/ (Méthode de calcule intégrales)
Salut,
Voilà quel est le principe du changement de variable :
Soient I et J deux intervalles de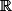 contenant plus de 2 points,
contenant plus de 2 points,
f une application de I dans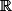 ,
,
 une application de J dans I,
une application de J dans I,  étant dérivable et de dérivée continue,
étant dérivable et de dérivée continue,
Alors pour tout ( ,
, )
) 
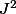 ,
,
 ^ {\phi(\beta)} f(t) dt) =
= )\phi'(u) du) ,
,
ce que l'on montre aisément en exprimant le terme de gauche à l'aide d'une primitive F de f, et en remarquant dans le terme de droite une forme f'*gof...

Voilà quel est le principe du changement de variable :
Soient I et J deux intervalles de
f une application de I dans
Alors pour tout (
ce que l'on montre aisément en exprimant le terme de gauche à l'aide d'une primitive F de f, et en remarquant dans le terme de droite une forme f'*gof...
"Je vous ai compris !"
Alleluia Gloria !
Merci pour cet éclaircissement. Quelle que soit l'orthodoxie de la méthode, elle a l'avantage d'être compréhensible aux yeux de la profane ébahie que je suis. (désolée Alpha, mais je n'ai absolument pas réussi à suivre ton explication... sûrement plus rigoureuse, mais également quasi incompréhensible pour moi.... cela dit c'est noté, et je me pencherai dessus plus tard pour voir ! merci beaucoup !!)
Merci également pour le lien, très instructif : je ne connaissais pas le tiers des "primitives usuelles" (dont celle à utiliser ici) , et ignore toujours la signification de certaines notations (arctan, etc. : mais ceci fera l'objet d'un autre topic :D )
Merci encore !
Au fait : était-il humainement possible de "primitiver" 1/sinx en n'utilisant que des formules ou astuces supposées connues en terminale s par un élève lambda ?
Merci pour cet éclaircissement. Quelle que soit l'orthodoxie de la méthode, elle a l'avantage d'être compréhensible aux yeux de la profane ébahie que je suis. (désolée Alpha, mais je n'ai absolument pas réussi à suivre ton explication... sûrement plus rigoureuse, mais également quasi incompréhensible pour moi.... cela dit c'est noté, et je me pencherai dessus plus tard pour voir ! merci beaucoup !!)
Merci également pour le lien, très instructif : je ne connaissais pas le tiers des "primitives usuelles" (dont celle à utiliser ici) , et ignore toujours la signification de certaines notations (arctan, etc. : mais ceci fera l'objet d'un autre topic :D )
Merci encore !
Au fait : était-il humainement possible de "primitiver" 1/sinx en n'utilisant que des formules ou astuces supposées connues en terminale s par un élève lambda ?
Jusqu'à preuve du contraire, je ne pense pas que c'était réalisable avec les moyens d'un élève de terminale.
En revanche, la formule que j'ai t'ai donnée plus haut se démontre en 2 petites lignes avec les moyens d'un élève de terminale.
Les histoires de continuité sont là pour être sûr que l'intégrale existe, mais ne doivent pas t'embrouiller.
;)
PS : pour le terme de gauche, lire intégrale de phi(alpha) à phi(beta).
En revanche, la formule que j'ai t'ai donnée plus haut se démontre en 2 petites lignes avec les moyens d'un élève de terminale.
Les histoires de continuité sont là pour être sûr que l'intégrale existe, mais ne doivent pas t'embrouiller.
;)
PS : pour le terme de gauche, lire intégrale de phi(alpha) à phi(beta).
en effet, ma formule proposée précédemment n'aboutissait à rien, j'ai même retournée la fonction dans tous les sens et j'en arrive à la conclusion que seul le changement de variable permet de s'en sortir.
Cependant, étant donné que la méthode du changement de variable n'est pas au programme de la Tle, je pense plus que l'exercice était plus une introduction au programme de maths-sup qu'une revision donc pas de reproche à te faire.
Disons que tu as mis une demie-phalange dans le programme de maths-sup
Cependant, étant donné que la méthode du changement de variable n'est pas au programme de la Tle, je pense plus que l'exercice était plus une introduction au programme de maths-sup qu'une revision donc pas de reproche à te faire.
Disons que tu as mis une demie-phalange dans le programme de maths-sup
Incroyable ! Tout s'éclaire !
Alpha a écrit:PS : pour le terme de gauche, lire intégrale de phi(alpha) à phi(beta).
ah ok c'est déjà plus clair comme ça !! (je ne comprenais pas ce que c'était : produit, puissance ou ...)
Merci encore !
Bah,au moins une demi-phalange qui ne sera pas bouffée toute crue par les piranhas , et une demi phalange avertie ....
Triderou a écrit:je pense plus que l'exercice était plus une introduction au programme de maths-sup qu'une revision donc pas de reproche à te faire.
et même si c'était supposé connu en terminale ... j'ai déjà abandonné ne serait-ce que l'idée d'être forte en maths donc pas de souci !
le magazine sus-cité évoquait la possibilité de faire un changement de variable, mais je n'avais pas compris ce passage. il expliquaient cela à partir d'un exemple :
pour calculer l'intégrale de 0 à 1 de 1/(racine de 2x+1)dx, on posait u(x)=racine de 2x+1 et on obtenait intégrale de 1 à racine de 3 du. tout ceci exposé sans calcul intermédiaire, comme si c'était une simple révision. ils ont tout de même pris la peine d'expliquer que si x parcourt [0,1] alors u parcourt [1,racine de 3] ...
autrement dit, cet exemple m'a embrouillé plus qu'autre chose, et je n'y avais strictement rien compris.....
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
