Identité de Bezout - Question
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
SeifMaths
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Oct 2016, 17:42
-
 par SeifMaths » 11 Mar 2017, 22:14
par SeifMaths » 11 Mar 2017, 22:14
Salut,

Je n'arrive pas à résoudre la dernière question c/ de l'exercice 1. Je n'ai trouvé que 217^18 congru à 1 mod 19 d'après Fermat et que 437=19*23
Nb: le résultat de b/ est x = 437 p + 400

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Mar 2017, 23:48
par Ben314 » 11 Mar 2017, 23:48
Salut,
Je suis pas très certain que ce soit exactement ça qui est attendu, mais une méthode, ça consiste à regarder à quoi est congru

modulo
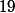
et
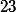
(vu que

).
- Modulo
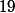
c'est super facile :

est premier et le petit théorème de Fermat te dit que pour tout

non divisible par

on a

. Donc comme

est non divisible par
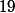
on a

.
- Par contre modulo

(qui est aussi premier), c'est plus la merde, mais c'est encore faisable "à la main" :

Donc
 (c'est là qu'il y a éventuellement une astuce qui m'a échappé vu que ce que la méthode que j'emploie, c'est plutôt de l'info que des maths.)
(c'est là qu'il y a éventuellement une astuce qui m'a échappé vu que ce que la méthode que j'emploie, c'est plutôt de l'info que des maths.)Conclusion :

est solution du système que tu viens de résoudre et donc le reste de la division de

par

c'est
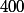
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
SeifMaths
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Oct 2016, 17:42
-
 par SeifMaths » 12 Mar 2017, 00:06
par SeifMaths » 12 Mar 2017, 00:06
Oui effectivement, le problème est au niveau du modulo 23, mais quand vous avez rédigé la méthode ça ne parait pas vraiment assez long, donc je crois que c'est la seule démarche possible (à mon niveau)
Merci pour la réponse!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mar 2017, 00:21
par Ben314 » 12 Mar 2017, 00:21
Y'a éventuellement une autre façon de faire qui évite de monter jusqu'à

:
Comme

est non divisible par
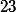
qui est premier on a

.
Or

(c.f. post précédent pour

)
Donc

est égal à l'inverse de
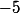
modulo
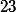
qu'on peut calculer soit "en tatonant", soit via l'algo. d'Euclide.
(par rapport à l'autre méthode, en terme de nombre de calculs, ça doit se valoir)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
SeifMaths
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Oct 2016, 17:42
-
 par SeifMaths » 12 Mar 2017, 00:45
par SeifMaths » 12 Mar 2017, 00:45
Ben314 a écrit:Y'a éventuellement une autre façon de faire qui évite de monter jusqu'à

:
Comme

est non divisible par
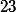
qui est premier on a

.
Or

(c.f. post précédent pour

)
Donc

est égal à l'inverse de
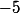
modulo
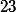
qu'on peut calculer soit "en tatonant", soit via l'algo. d'Euclide.
(par rapport à l'autre méthode, en terme de nombre de calculs, ça doit se valoir)
Ah oui, je crois qu'il suffit de trouver

est égal à l'inverse de
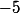
modulo
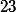
pour dire qu'en multipliant -5 par 9 on trouve 1 d'où

est congru à

modulo
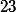
?
-
aviateur
 par aviateur » 12 Mar 2017, 00:55
par aviateur » 12 Mar 2017, 00:55
On peut encore simplifier malgré tout
1. Avec 217=230-13 d'où (avec le binôme de Newton)
217^18=13^18 mod 23
[En effet (230-13)^18=(13-230)^18=13^218+ multiples de 23.]
On arrive + vite a 13^4=-5 mod 23
2. Et puis voir que 9*5=45=2*23-1 d'où l'inverse de -5 c'est 9 (mod 23)
Modifié en dernier par aviateur le 12 Mar 2017, 14:05, modifié 1 fois.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mar 2017, 00:56
par Ben314 » 12 Mar 2017, 00:56
SeifMaths a écrit:Ah oui, je crois qu'il suffit de trouver

est égal à l'inverse de
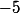
modulo
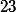
pour dire qu'en multipliant -5 par 9 on trouve 1 d'où

est congru à

modulo
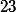
?
Oui, c'est ça.
Aprés, c'est vrai que le 9 tu le "sort un peu d'un chapeau", mais tu peut toujours dire que vu le début de l'énoncé c'est un peu normal de commencer par regarder si "par hasard" ça serait pas lui qui marche.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités


:
est non divisible par
qui est premier on a
.
(c.f. post précédent pour
)
est égal à l'inverse de
modulo
qu'on peut calculer soit "en tatonant", soit via l'algo. d'Euclide.
est égal à l'inverse de
modulo
pour dire qu'en multipliant -5 par 9 on trouve 1 d'où
est congru à
modulo
?