Fonctions+suites

par **julie55** » 21 Nov 2006, 18:19

bonsoir c moi!!

jai un problème je ne comprend pas:

Exercice1:

1)on considère ,pour chaque entier n>=2,la fonction Fn définie sur R+ par
Fn(x)=x^(n+1)+x^n+x²+x-1 et sa coube représentative Cn.

a)Etudier les variation et représenter graphiquement F2,F3,F4.
b)montrer que les fonction Fn son strictmen croissante et que les courbes Cn on 2 points en communs
c)Montrer que Fn(x)=0 a une solution unique que lon notera Un

2)a)calculer U2 puis donner une valeur approchée par défaut a 10^-3 près de U3,U4,U10.
b)montrer que les terme de la suite sont dans ]0;2/3[
c)en comparant Fn et F(n+1) sur [0;1] montrer que Und)en déduire que la suite est croissante et kelle converge.

la 1ere partie jai tout fait mais c la 2eme partie qui me pose problème comment calculer U2 alors que lon a pas Un??on sait juste que 0<=Un c tout
alors coment faire??
et comment faire pour la b) là je ne vois même pas du tout je nai aucune piste
la c) est-ce que lon dire que comme Fnet pour la d) je saurais faire.

par **julie55** » 22 Nov 2006, 10:01

quelqun peut maider?? :cry: je ne comprend vraiment pas??? :hein:

par **julie55** » 23 Nov 2006, 17:02

2)a)calculer U2 puis donner une valeur approchée par défaut a 10^-3 près de U3,U4,U10.
pour cette question je croit avoir trouver mais je suis pas sure:
fn(Un)=0 alors f2=(U2)= mais same donne

F2(x)=x^3+x^2+x²+x-1 alors comment faire ???

aidez moi silvouplait :cry: :cry: est -ce je suis dans la mauvaise voie

on a mm pas de formule pour Un comment faire au moin pour trouver Un parce que je ny arrive vraiment pas!! :cry: :cry:

par **julie55** » 23 Nov 2006, 18:11

2)a)calculer U2 puis donner une valeur approchée par défaut a 10^-3 près de U3,U4,U10.
pour cette question je croit avoir trouver mais je suis pas sure:
fn(Un)=0 alors f2=(U2)= mais same donne

F2(x)=x^3+x^2+x²+x-1 alors comment faire ???

aidez moi silvouplait est -ce je suis dans la mauvaise voie

on a mm pas de formule pour Un comment faire au moin pour trouver Un parce que je ny arrive vraiment pas!!

par **maturin** » 23 Nov 2006, 18:25

pour la question 1 il faut faire une étude de fonction avec tableau de variation.

tu verras que la dérivée est stricement positive donc la fonction est strictement croissante.
elle est négative en 0 positive pour x>1, donc elle s'annule une seule fois sur [0,1] en un point que l'on note Un.

U2 est tel que f2(U2) = 0
c'est une équation du 3eme degrè à resoudre (tu es sure que tu t'es aps trompée et que fn=x^n+...+x-1 ? ainsi tu aurais du 2nd degré)

pour U3,U4,U10 tu cherche x pour que f3(x) proche de 0 c'est à dire tu dois trouver x tel que f3(x-0.001)<0 et f3(x+0.001)>0
pour cela y a pas de méthode miracle, faut le faire à tatons (c'est un peu bourrin ton exo...)

par **julie55** » 23 Nov 2006, 19:51

re!

U2 est tel que f2(U2) = 0
c'est une équation du 3eme degrè à resoudre (tu es sure que tu t'es aps trompée et que fn=x^n+...+x-1 ? ainsi tu aurais du 2nd degré)

dabord merci tu es le 1er a me répondre

et non jme suis pas trompé pour la fonction fn c bien:

Fn(x)=x^(n+1)+x^n+x²+x-1

il me demande de calculer U2,a mon avis ce nest pas une valeur approchée quil me demande et c sa qui membète et je ne sais pas quoi faire... :briques:

mais je crois avoir trouver grace a ton aide tu ma donné une piste ...merci :++:

par **julie55** » 24 Nov 2006, 13:08

en faite je nai pas trouvé est-ce que lon pourrait pas prndre la dérivée de Fn pour calculer U2 sa marrangerai bien???

F2(x)=x^3+x^2+x²+x-1 ou alors faut résoudre cet équation mais c du 3eme degré donc c un peu dur jai essaye de voir si il ny a vait pas une identité remarquable mai jai vérifié jai tout essayé sa marche pas!!sa menerve!pouvez vous seulement me donner une petite piste pour démarrer silvouplait parce que jai tout essayé sa marche pas et c en train de ménerver... :cry: :cry:

merci beaucoup pour tout aide :marteau: :mur:

par **julie55** » 24 Nov 2006, 13:11

U2 est tel que f2(U2) = 0
c'est une équation du 3eme degrè à resoudre

c'est Fn(Un)=0 donc F2(U2) n'est pas égal a 0 mais pouvez vous mexpliquer silvouplait sa serai gentil :briques:

merci

par **julie55** » 24 Nov 2006, 16:03

--------------------------------------------------------------------------------

en faite je nai pas trouvé est-ce que lon pourrait pas prndre la dérivée de Fn pour calculer U2 sa marrangerai bien???

F2(x)=x^3+x^2+x²+x-1 ou alors faut résoudre cet équation mais c du 3eme degré donc c un peu dur jai essaye de voir si il ny a vait pas une identité remarquable mai jai vérifié jai tout essayé sa marche pas!!sa menerve!pouvez vous seulement me donner une petite piste pour démarrer silvouplait parce que jai tout essayé sa marche pas et c en train de ménerver...

merci beaucoup pour tout aide

par **maturin** » 24 Nov 2006, 16:34

ben ça me parait vraiment bizarre ton ennoncé si on te demande de calculer u2 de manière exacte.
Car pour les équations du 3eme degré normalement t'es pas sensé connaître les racines surtout si elles sont pas évidentes (là u2~0.466).

sinon si c'est vraiment ça faut te ramener à la formule de Cardan en faisant un changement de variable x=u-2/3:

mais je suis pas sûr que ce soit à ton programme, et je suis aps sûr que ça soit très intéressant...

par **julie55** » 24 Nov 2006, 16:41

Car pour les équations du 3eme degré normalement t'es pas sensé connaître les racines surtout si elles sont pas évidentes (là u2~0.466).

comment a tu fait pour calculer U2??parce que je ne vois vraiment pas comment tu a fait..et je suis déséspérée là... :triste:

par **maturin** » 24 Nov 2006, 16:46

en gros tu trouves

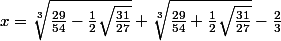
et moi j'appelle pas ça une racine évidente :zen:

par **maturin** » 24 Nov 2006, 16:50

mais la première méthode que j'ai utilisée est la dichotomie pour trouver une valeur approchée.
(ou alors t'as un logiciel qui peut te tracer ta courbe et qui puisse te permettre de zoomer sur l'intersection de cette courbe avec l'axe des x)

enfin pour u3, u4 et u10 y a pas de formule, t'es obligée de faire à taton, par dichotomie, par méthode de newton ou autre méthode plus ou moins informatisée.

par **julie55** » 24 Nov 2006, 16:56

pour faire U3 etc c la méthode par balayage en faite??

par **julie55** » 24 Nov 2006, 17:04

jai vérifié avec un logiciel pour U2 sa me donne exactement 8/17(jai zoomé comme tu ma dit) et jai trouvé sa

enfin pour u3, u4 et u10 y a pas de formule, t'es obligée de faire à taton, par dichotomie, par méthode de newton ou autre méthode plus ou moins informatisée.

tu peut me donner un exemple??parce que on ne sait pas ou U3 se trouve ...(jarriverai jamais a comprendre!!! :briques: )

par **maturin** » 24 Nov 2006, 17:06

je sais pas ce que t'appelle méthode de balayage.
pour la dichotomie, c'est quand tu cherches f(x)=0 avec f croissante

si tu as f(a)0
tu calcule le signe de

si c'est positif alors

sinon

et tu recommences sur ce nouvelle intervalle. A chaque fois tu divise la taille de ton intervalle par 2. Quand ton intervalle fera moins de

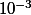
tu pourras t'arrêter et tu auras ton approximation.

par **maturin** » 24 Nov 2006, 17:11

julie55 a écrit:jai vérifié avec un logiciel pour U2 sa me donne exactement 8/17(jai zoomé comme tu ma dit

alors sauf si la formule que tu as utilisée n'est pas celle que tu as donné, la valeur exacte de u2 est celle que j'ai donnée au dessus pour le x avec les racines cubiques.

maintenant 8/17~0.47 est une valeur approchée à

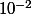
près.
donc continu de zoomer pour les

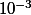
:we:

Fonctions+suites

fonctions+suites

silvouplait

toujour ce problème qui membète!!

silvouplai aidez moi

Qui est en ligne