Exo géométrie seconde
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Loumares
- Messages: 2
- Enregistré le: 03 Nov 2018, 11:55
-
 par Loumares » 03 Nov 2018, 23:25
par Loumares » 03 Nov 2018, 23:25
Soit un triangle MDR rectangle en M tel que MD=4 et MR=3 . N est un point du segment DR. Les points S et T appartiennent respectivement aux segments MD et MR tels que le quadrilatère MSNT soit un rectangle.
Où faut-il placer le point N sur le segment DR pour que le rectangle MSNT soit un carré?
Je bloque à cet exo, j’ai essayé plusieurs fois et je bloque toujours si qq’un pouvait me guider, merci.

-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 04 Nov 2018, 09:15
par titine » 04 Nov 2018, 09:15
Tu veux que MSTN soit un carré. C'est à dire que MS=MT. (Ou que NS=TN.)
Tu veux savoir qu'elle est la position de N sur [DR] dans ce cas là.
Appelle par exemple x la longueur RN.
1) comme (NS) parallèle à (RM), d'après Thales : NS/RM=DN/DR
RM=3 ; DR=5 d'après Pythagore et DN=5-x
2) comme (TN) parallèle à (MD), d'après Thales : TN/MD=RN/RD
MD=4 ; RN=x et RD=5
Donc tu peux exprimer NS et TN en fonction de x puis chercher pour qu'elle valeur de x on a NS=TN en résolvant une équation.
C'est bon ?
-
aviateur
 par aviateur » 04 Nov 2018, 14:50
par aviateur » 04 Nov 2018, 14:50
Bonjour
Dans cet exercice on peut éviter les calculs et c'est toujours préférable à mon avis.
D'après les symétries du carré, pour que MSNT en soit un, il faut que N soit à l'intersection de [DR] et

où
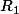
est sur [MD] et
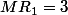
et

est sur
)
et
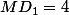
. Cela donne la réponse directement sans se fatiguer.
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 04 Nov 2018, 15:09
par titine » 04 Nov 2018, 15:09
Oui, tout à fait d'accord !
Comme souvent il y a plusieurs méthodes possibles pour résoudre ce problème.
La méthode purement géométrique est en effet sans doute plus élégante.
-
aviateur
 par aviateur » 04 Nov 2018, 16:07
par aviateur » 04 Nov 2018, 16:07
En fait j'ai pas fait les calculs. Mais je ne serai pas étonné que' le problème se ramène à une équation du second degré. Et d'un point de vue pédagogique c'est pas inutile de mettre en équation aussi.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités