Exercice sur les fonctions dérivées
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tsukindustries
- Membre Relatif
- Messages: 113
- Enregistré le: 31 Déc 2006, 05:44
-
 par tsukindustries » 25 Jan 2009, 02:35
par tsukindustries » 25 Jan 2009, 02:35
Bonjour et merci d'avance de votre aide sur cet exercice sur les fonction derivees.
Determiner l'intervalle (ou la reunion d'intervalles) de

sur lequel la fonction
f est derivable et calculer sa derivee.
1)
 = \frac{-7}{\sqrt{2x+1}})
2x+1 > 0 2x > -1 x >
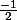 f
f est derivable sur ]
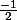
;+

[
f =
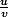
u(x) = -7
u'(x) = 0
v = ?
Que dois je mettre quand il y a une racine! C'est ma grosse intrigue! 2)
 = \frac{cos x}{3{x}^{2}})
3

=0

=0 x = 0
f est derivable sur ]-

;0[;]0;+

[
f =
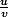
u(x) = cosx
u'(x) = -sinx
v(x) =

v'(x) = 6x
f =
 f
f(x) = -3

(sinx) - 6x(cosx)
f(x) = -3x(x(sinx) + 2(cosx))
Est ce bon? 3)
 = (3x+1)\sqrt{3x+1})
3x+1 > 0 2x > -1 x >
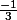 f
f est derivable sur ]
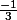
;+

[
f = uv
u(x) = 3x+1
u'(x) = 3
v(x) = ?
J'ai encore le meme probleme, pouvez vous m'expliquer comment il faut faire?
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 25 Jan 2009, 08:19
par fibonacci » 25 Jan 2009, 08:19
Bonjour;
Rappels :
^,=2x)
on peut avoir une constante a en facteur.
^,=2ax)
et quelque soit n.
^,=nx^{n-1})
^,=anx^{n-1})
}^\prime=\left({x^{\frac{1}{2}}}\right)^\prime=\frac{1}{2}x^{\frac{1}{2}-1}=\frac{1}{2}x^{-\frac{1}{2}}=\frac{1}{2\sqrt{x}})
on aurait pu écrire :
^,=nu^{n-1}u^,)
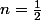
avec
^\prime=\frac{1}{2}x^{\frac{1}{2}-1}\time 1=\frac{1}{2\sqrt{x}})
=-7\frac{1}{\sqrt{2x+1}}=-7\frac{1}{\sqrt{2x+1}}=-7{\frac{1}{\sqrt{w}})
'=-7(-\frac{1}{2})(w^{-\frac{1}{2}-1})w')
pour la 2 où est passé le dénominateur ?
-
tsukindustries
- Membre Relatif
- Messages: 113
- Enregistré le: 31 Déc 2006, 05:44
-
 par tsukindustries » 25 Jan 2009, 13:43
par tsukindustries » 25 Jan 2009, 13:43
Merci beaucoup!
1)
 = \frac{-7}{\sqrt{2x+1}})

f est derivable sur

= -7 \times \frac{1}{\sqrt{2x+1}})

v(x)

v'(x)

f'

f'(x)

f'(x)
\sqrt{2x+1}}) Est ce que je dois a la fin multiplier par le -7 que j'avais laisse?
Est ce que je dois a la fin multiplier par le -7 que j'avais laisse?
Je me demande ca parce que qd je fais avec f = uv
Je trouve f'(x)
\sqrt{2x+1}})
3)
 = (3x+1)\sqrt{3x+1})

f est derivable sur
 L'intervalle doit - il bien etre ouverte sur
L'intervalle doit - il bien etre ouverte sur 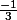 ?
?f = uv
u(x) = 3x+1
u'(x) = 3
v(x) =

v'(x) =

f' = u"v+uv"
f'(x)
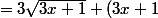\frac{3}{2\sqrt{3x+1}})
f'(x)

f'(x)

f'(x)

f'(x)
}{2\sqrt{3x+1}})
2)
 = \frac{cos x}{3{x}^{2}})
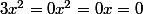
f est derivable sur


u(x)

u'(x)

v(x)

v'(x)

f'

f'(x)
 - 6x(cosx)}{9{x}^{4}})
f'(x)
 -2(cosx))}{9{x}^{4}})
f'(x)
 - 2(cosx)}{3{x}^{3}})
Est ce bon?? Merci d'avance

-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 25 Jan 2009, 14:38
par fibonacci » 25 Jan 2009, 14:38
Bonjour;
Excellent, quelques détails.
1
\sqrt{2x+1}})
3
}{2\sqrt{3x+1}}=\frac{9\sqrt{3x+1}}{2})
2

et non

et

attention à l'lécriture.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 170 invités
