Etude de fonction exponentielle TS

[nisha]

Bonsoir à tous! j'ai besoin d'aide sur un exercice type BAC d'après le professeur. Je crois avoir réussi la première moitié et c'est sur la seconde moitié que j'ai besoin de vous. (je vous exposerez ma reponse après l'énoncé pour que vous puissiez vérifier si le début de l'exercice est bon) Alors voilà:


1. Etudier le fonction f définie sur R par :
F(x)= x + 1 - ex
Représenter graphiquement cette fonction dans un repère orthonormal et préciser l’asymptote oblique.
2. Soit lamda un nombre réel et la fonction f lamda définie par
f lamda (x)= lamda( x + 1 ) - ex (exp de x)
On note G lamda la courbe représentative de f lamda . Trouver l’ensemble des valeurs de lamda pour lesquelles f lamda admet un maximum. Soit M lamda le point d’ordonnée maximale de G lamda , donner une équation de l’ensemble des points M lamda .

Voilà ce que je trouve:
1) f(x)=x+1-ex
f définie et dérivable sur
f '(x)=1-ex
Signe de f '(x) :
f '(x)>0 1-ex>0 ex<1 x<0 f croissante
f '(x)<0 1-ex<0 ex>1 x>0 f décroissante
f '(x)=0 1-ex=0 ex=1 x=0 maximum de f

Lorsque x tend vers - l'infini, ex tend vers 0 donc y=x+1 est l'équation de l'asymptote oblique.

2) f (x) = lamda(x+1)-ex
f ' (x) = lamda - ex

Voilà! c'est là que je bloque! comment continuer? et qu'est-ce que je dois trouver ? Comment faire pour trouver le maximum ainsi que l'équation de l'ensemble des points de M ? ça à surement un lien avec le début de l'exercice mais le problème c'est qu'il faut savoir le montrer. j'espère que vous pourriez m'aider et merci d'avance! A+

[nisha]

Resalut! Alors personne ne peut vraiment pas m'aider ? vous savez, une toute petite indication serait la bienvenue alors n'hésiter pas même si c'est quelque chose pas sûr, je veux juste une idée qui pourrait m'ammener sur la voie car je suis complétement bloquer! j'ai beau :mur: mais néant alors s'il vous plaît :help: et merci d'avance!

[Quidam]

Salut,

Tu as brillamment résolu la première question, où est le problème pour la deuxième ?

C'est bon !
A quelle condition la courbe aura-t-elle un maximum ? A condition que f' s'annulle, c'est-à-dire s'il existe x tel que :


soit


Ceci n'est possible que si , mais dans ce cas :



Le point maximum est donc :







Et pour trouver le lieu de ces points maximum, essaie de trouver une relation entre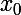 et qui ne dépende pas de !

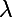Courage !