équation second degré avec racine carrée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
cloudinet
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Oct 2013, 21:01
-
 par cloudinet » 12 Oct 2013, 21:12
par cloudinet » 12 Oct 2013, 21:12
Bonjour, j'ai un petit souçis pour trouver la méthode avec une équation du second degré:
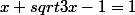
Moi j'ai juste mis le x de l'autre coté puis tout mis au carré ce qui fait 3x-1 = 1-2x+x^2
donc au final x^2-5x+2=0
je trouve deux racines
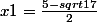
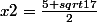
j'ai vérifié sur la calculette et je voudrais savoir pourquoi x2 est faux, merci d'avance de votre aide.
-
Slaker
- Membre Naturel
- Messages: 91
- Enregistré le: 17 Mar 2013, 13:28
-
 par Slaker » 12 Oct 2013, 21:20
par Slaker » 12 Oct 2013, 21:20
x2 est juste
-
cloudinet
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Oct 2013, 21:01
-
 par cloudinet » 12 Oct 2013, 21:46
par cloudinet » 12 Oct 2013, 21:46
Pourtant si je tape sur la calculette
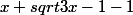
(et non
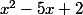
où j'étais arrivé), la courbe ne coupe en aucun cas l'axe des abscisses pour une valeur aussi grande que x2.
C'est bizarre non :/? même si je sais bien qu'en partant de là x peut prendre moins de valeurs, de là à changer complètement la forme de la courbe... à bien y regarder je pense pas qu'elle passe non plus par mon x1, c'est peut-être dans les manips pour en arriver à ma seconde expression que j'ai fait une erreur, mais je vois pas où.
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 12 Oct 2013, 22:13
par annick » 12 Oct 2013, 22:13
Bonjour,
je suis d'accord avec tes constatations sur la calculette.
Il me semble qu'il y a un petit problème de domaine de définition.
Si tu poses :
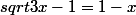
tu dois avoir 1-x>0 car une racine est toujours positive.
Donc il faut x<1. C'est le cas de x1, mais pas de x2, donc cette dernière solution est à éliminer, ce qui colle bien avec le graphique que l'on voit sur la calculatrice.
-
cloudinet
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Oct 2013, 21:01
-
 par cloudinet » 12 Oct 2013, 22:26
par cloudinet » 12 Oct 2013, 22:26
Le principe est simple à appliquer mais le concept en lui-même me semble compliqué.
Car du coup, quand on met au carré on a un parti-pris non? (on raisonne par implication et pas par équivalence si j'ai bien saisi), et pour les cas où 1-x serait <0 on ne peut rien vérifier/résoudre? C'est un peu tordu mais j'aimerais saisir.
-
coote
- Membre Relatif
- Messages: 138
- Enregistré le: 26 Avr 2012, 01:15
-
 par coote » 12 Oct 2013, 23:10
par coote » 12 Oct 2013, 23:10
cloudinet a écrit:Pourtant si je tape sur la calculette
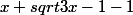
(et non
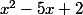
où j'étais arrivé), la courbe ne coupe en aucun cas l'axe des abscisses pour une valeur aussi grande que x2.
C'est bizarre non :/? même si je sais bien qu'en partant de là x peut prendre moins de valeurs, de là à changer complètement la forme de la courbe... à bien y regarder je pense pas qu'elle passe non plus par mon x1, c'est peut-être dans les manips pour en arriver à ma seconde expression que j'ai fait une erreur, mais je vois pas où.
sachez que certaine equation demande un domaine de travail avant la resolution
a votre niveau il y a celles qu'il contiennent un racine carre et d'autres qui contiennent les fractions en x evidement.
lorsque tu respecte le domaine de travail, les solutions doivent obligatoirement repondre a votre resolution
ici d'autre exemple d'equation
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
(et non
où j'étais arrivé), la courbe ne coupe en aucun cas l'axe des abscisses pour une valeur aussi grande que x2.