Drotie D'Euler

[Zack-Fair]

On considère un triangle ABC avec :

A (1,2)
B(3,-1)
C(-4,4)

a) Détermine les coordonnées de l'orthocentre et du centre du cercle circonscrit.
b)Détermine l'équation de la droite passant par ces 2 points.
c)Comment s'appelle cette droite ?
d) Quel autre point particulier à également cette droite ? ( juste son nom )



REPONSES AUX QUESTIONS:

a)

- Je trouve les coordonnés de l'orthocentre :

hauteur issue de C => 3y + 4x + 4 = 0
hauteur issue de B => 2y - 5x + 17 = 0

Je résous un système pour trouver l'orthocentre et j'obtiens pour les
x : 43/23
y : -88/23

-- Je trouve les coordonnés de cercle circonscrit :
BC => 10y - 7x + 18 =0
Ac => 15y - 10x -11 = 0


Je résous un système pour trouver le centre de gravité et j'obtiens pour les
x : 70
y: 257/5


b) j'ai pensé qu'on parlait de Euler donc j'ai calculer le coefficient angulaire grace à mes deux coordonnées mais j'obtiens une réponse pas possible quoi ...

c) Euler

d) Le centre de gravité


Voilà , ça fait 2 heures que je suis la dessus , j'ai recommencé mes calculs x fois mais je galère toujours , j'ai des réponses qui ne sont pas logiques :hum:


Quelqu'un aurait-il la gentillesse de m'aider à résoudre ces exercices ?


Merci d'avance

[Dinozzo13]

Salut !

Je n'ai pas fait les calculs mais, pour la b) si tu veux trouver l'équation de cette droite, rien de plus simple :
Tu connais les coordonnées de l'hortocentre H et du cetnre du cercle circonscrit \Omega donc trouve les coordonnées de
Tu en déduis ensuite une équation cartésienne de :
où tu as calculé
Il te faut juste trouver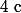 . Pour cela tu dis que H appartient à donc ses coordonnées vérifient l'équation de cette droite, déduis-en c et voilà

[Zack-Fair]

Je n'ai pas très bien compris les formules , peux tu me les remplacer par les nombres que j'ai stp ? Comme ça je les fait et je dit quoi :happy2:

[Dinozzo13]

Quels sont les coordonnées du point :
- H orthocentre de ton triangle ?
- centre du cercle circonscrit ?

[Zack-Fair]

Pour l'orthocentre :
x : 43/23
y : -88/23


Pour le centre du cercle circonscrit :
x : 70
y: 257/5

[Dinozzo13]

désignant les coordonnées de H et désignant les coordonnées de

Tu n'as qu'à remplacer dasn ce que j'ai mis ^^

[Zack-Fair]

Donc ça donne :

(43/23 - 70 ; -88/33 - 257/5 ) => ( 43/23 -1610/23 ; -880/33 - 8481/33)

(1567/23 ; 9361/33 )

Je m'arrete là car j'obtiens des coordonnées impossible..

Peux tu m'aider ?

[Dinozzo13]

tu t'es peut-être trompé(e) au début lors de la détermination des équations des hauteurs, repars de zéro et explique to nraisonnment.

[Zack-Fair]

Hauteur issue de C

coeff ang AB : -1-2/3-1 = 3/4 comme c'est perpendiculaire : -4/3

équation de la hauteur :

y-4 = -4/3 ( x+4)
y-4= -4x/3 -16/3
3y -12 + 4x +16 =0

3y + 4x + 4 = 0


Hauteur issue de B

coeff ang de AC : 4-2/-4-1 =2/-5 comme c'est perpendiculaire : 5/2

équation de la hauteur :

y + 1 = 5/2 ( x - 3 )
y + 1 = 5x/2 -15/2
2y +2 -5x +15 = 0

2y -5x +17 = 0


Système pour trouver l'orthocentre :

3y + 4x +4 = 0
2y - 5x +17 = 0

6y +8x +8 -6y + 15x -51 = 0
23xx -43 = 0

x = 43/23

15y +20x +20 + 8y + 20x + 68 = 0
23y +88 =0

y = -88/23


Médiatrice de BC

Calcul du milieu :

3-4/2 ; -1-4/2 = ( -1/1;-5/2)

coeff angul . 4+1/-4-3 = 5/-7 = 7/5

équation de la droite :

y +5/2 = 7/5 (x+1/2)
y+5/2 = 7x/5 +7/10
10y + 25 - 7 -7x = 0

10y -7x +18 =0



Médiatrice de AC

calcul du milieu :

1-4/2 ; 2-4/2 = (-3/2 ; -1)

coeff angul. : 4-2/-4-1 = 2/5 = 5/2

équation de la droite :

y+1 = 5/2 (x+3/2)
y+1 = 5x/2 + 15/4
15y +4 -10x -15 =0

15y -10x -11 = 0

système pour trouver le centre du cercle circonscrit :

15y-10 -11 =0
10y-7x+18 = 0

30y -20x -22 -30y +21x -48 =0

x= 70

105y -70 x -77 -100y + 70x -180
5y -257 = 0

y= 257/5
---------------------------------------------------


Voilà ; c'est ça mon raisonnement , si on pouvait m'aider à résoudre cet exercice , ça serait sympa car franchement , je cherche depuis hier mais rien..

[Dinozzo13]

quand tu met "coeff ang AB" tu veux dire le coefficient directeur ?
Si c'est le cas, alors il est faut :
Si tu a et alors le coefficient de la droite (AB) vaut et non pas

[Zack-Fair]

A (1,2) et B (3,-1)

Je recherche le coefficient angulaire de AB et la formule c'est :

yb - ya / xb - xa ce qui donne

-1 -2 / 3 - 1 = -3/2 et la hauteur qui va passer par là à un coefficient angulaire inverse et opposé , ce qui donne 2/3

[Zack-Fair]

Personne pour m'aider ?

[Dinozzo13]

Corrige le reste, en fonction de ça, en particulier les autres équations de droites

[Zack-Fair]

je n'y arrive toujours pas :/