Devoir de mathématique seconde

[Mamaly]

Tout d'abord, bonjour et mer ci de prendre la peine de regarder ce texte dans le but de m'aider.
J'ai un DM de maths à rendre pour lundi et je n'arrive pas à faire le quatrième exercice correctement.
L'énoncé est:
Soit f, la fonction définie sur R par: f(x)=1/(x^2+1)
Il fallait copier et compléter un tableau de valeur, ce que j'ai fait sans problème.
Ensuite il fallait proposer une conjecture, ce que j'ai fait:
La fonction f est croissante sur ]-infini;0]
Il fallait ensuite la vérifier et c'est là que je croit m'être plantée.
Pour tous nombre u et v dans R, uf(u)=1/(u^2+1)
f(v)=1/(v^2+1)
f(u)-f(v)=[1/(u^2+1)]-[1/(v^2+1)]
Cette expression est inférieur à 0 donc f(u)Mais après je n'ai pas du tout compris comment faire pour la 2)
2) En enchainant les propriétés de la fonction carré et de la fonction inverse, montrer que f est décroissante sur [0;+infini[
Et je n'ai malheureusement pas appris ces propriétés....
Ensuite il fallait faire un tableau de valeurs de f pour x égal à 1/3;1/2;2;4;5;7
Mais après j'ai réussi. :++:
Ainsi je vous demande votre aide..

[SaintAmand]

Et je n'ai malheureusement pas appris ces propriétés...

Pas étonnant que tu n'y arrives pas. Apprends les.

Une autre solution consiste à montrer que la courbe représentative de la fonction f est symétrique par rapport à l'axe des ordonnées (on dit que la fonction est paire), c'est-à-dire que pour tout réel x, on a f(-x) = f(x).

[Mamaly]

Merci, et je ne les ai pas appris car j'étais absente pendant une semaine... ^^
Et mon professeur, dois-je préciser à un cour très mal structurer donc si quelqu'un connaît de bon site pour compléter mon apprentissage, je suis preneuse. En tout cas merci. :)

[SaintAmand]

Merci, et je ne les ai pas appris car j'étais absente pendant une semaine... ^^

Dans ton manuel, il y a évidemment toutes les propriétés que tu dois connaître au sujet des fonctions carré et inverse.

donc si quelqu'un connaît de bon site pour compléter mon apprentissage, je suis preneuse.

Ce n'est pas un bon site qu'il faut, mais un bon manuel. Ceux d'aujourd'hui ne valent rien. Dans ton CDI tu devrais pouvoir trouver des manuels très corrects des années 80.

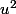
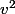
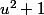
Pour en revenir à ton problème, prends u et v deux nombres réels positifs tels que u<v. Compare et , puis et , et enfin et .

[Mamaly]

Merci beaucoup.