Développement limité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 02 Sep 2008, 20:30
par farator » 02 Sep 2008, 20:30
Salut ! petite question :
Comment on montre que

est environ égal à
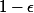
?
Merci
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 02 Sep 2008, 20:42
par le_fabien » 02 Sep 2008, 20:42
J'ai un peu oublié comment faire mais:
si je pose f(x)=
^a)
et grâce à l'approximation en zero faite en première on a f(x)=f(0)+xf'(0)+xe(x) alors on a f(x)=1+xa+xe(x)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Sep 2008, 20:48
par leon1789 » 02 Sep 2008, 20:48
farator a écrit:Salut ! petite question :
Comment on montre que

est environ égal à
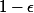
?
Merci
(1-\epsilon)} = \frac{1-\epsilon}{1-\epsilon^2})
Si

est proche de 0, que dire de
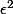
?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Sep 2008, 20:48
par leon1789 » 02 Sep 2008, 20:48
LEFAB11 a écrit:J'ai un peu oublié comment faire mais:
si je pose f(x)=
^a)
et grâce à l'approximation en zero faite en première on a f(x)=f(0)+xf'(0)+xe(x) alors on a f(x)=1+xa+xe(x)
C'est compliqué ton truc...
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 02 Sep 2008, 20:48
par farator » 02 Sep 2008, 20:48
Merci de répondre
Et comment arriver à

environ égal à
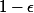
à partir de la formule
)
environ égal à
+\epsilon.f'(x))
?
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 02 Sep 2008, 20:49
par le_fabien » 02 Sep 2008, 20:49
leon1789 a écrit:(1+\epsilon) = 1 - \epsilon^2)
Si

est proche de 0, que dire de
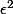
?
Bizarre ton truc!

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Sep 2008, 20:50
par leon1789 » 02 Sep 2008, 20:50
LEFAB11 a écrit:Bizarre ton truc!
J'ai modifié pour davantage de clarté... :we:
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 02 Sep 2008, 20:51
par le_fabien » 02 Sep 2008, 20:51
farator a écrit:Merci de répondre
Et comment arriver à

environ égal à
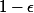
à partir de la formule
)
environ égal à
+\epsilon.f'(x))
?
Et bien
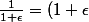^{-1})
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 02 Sep 2008, 20:54
par farator » 02 Sep 2008, 20:54
Ah et on peu utiliser la formule du binome ?
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 02 Sep 2008, 21:01
par le_fabien » 02 Sep 2008, 21:01
Bon je reprends :
f(

)=

et f'(

)=
^2})
et donc pour

petit
f(

)=f(0)+

f'(0)=1-

(à la place de " = " il faut lire " à peu près " car mes notions LaTex sont nouvelles)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Sep 2008, 21:02
par leon1789 » 02 Sep 2008, 21:02
Finalement, mon premier message était le bon, je n'aurais pas dû changer...
(1-\epsilon) = 1 -\epsilon^2)
(quelle complexité !)
si

est proche de 0, alors
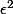
est
négligeable !
Donc
(1-\epsilon) = 1 -\epsilon^2 \simeq 1)
et le résultat tombe :
)
et
)
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 02 Sep 2008, 21:08
par le_fabien » 02 Sep 2008, 21:08
leon1789 a écrit:Finalement, mon premier message était le bon, je n'aurais pas dû changer...
(1-\epsilon) = 1 -\epsilon^2)
(quelle complexité !)
si

est proche de 0, alors
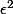
est
négligeable !
Donc
(1-\epsilon) = 1 -\epsilon^2 \simeq 1)
et le résultat tombe :
)
et
)
Ok mais si

est déjà négligeable , comment fait-on ? :we:
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 02 Sep 2008, 21:11
par farator » 02 Sep 2008, 21:11
leon1789 a écrit:Finalement, mon premier message était le bon, je n'aurais pas dû changer...
(1-\epsilon) = 1 -\epsilon^2)
(quelle complexité !)
si

est proche de 0, alors
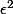
est
négligeable !
Donc
(1-\epsilon) = 1 -\epsilon^2 \simeq 1)
et le résultat tombe :
)
et
)
tu considères e² négligeable, donc pourquoi pas e ??

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Sep 2008, 21:13
par leon1789 » 02 Sep 2008, 21:13
LEFAB11 a écrit:Ok mais si

est déjà négligeable , comment fait-on ? :we:
heu...

négligeable devant quoi ?
Je disais que
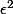
est négligeable (devant

quand ce dernier est proche de 0)
Maintenant, si on néglige totalement

, alors on obtient

, ce qui n'est pas faux, mais ce qui ne sert pas à grand chose :we:
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 02 Sep 2008, 21:15
par farator » 02 Sep 2008, 21:15
Remarque c'est pas faux on s'arrête à l'ordre 1

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Sep 2008, 21:16
par leon1789 » 02 Sep 2008, 21:16
farator a écrit:Remarque c'est pas faux on s'arrête à l'ordre 1
oui, c'est lié à ça effectivement.
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 02 Sep 2008, 21:16
par le_fabien » 02 Sep 2008, 21:16
LEFAB11 a écrit:Bon je reprends :
f(

)=

et f'(

)=
^2})
et donc pour

petit
f(

)=f(0)+

f'(0)=1-

(à la place de " = " il faut lire " à peu près " car mes notions LaTex sont nouvelles)
Voilà pourquoi je préfère cela, pour moi c'est plus clair.
Votre avis ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Sep 2008, 21:19
par leon1789 » 02 Sep 2008, 21:19
LEFAB11 a écrit:Voilà pourquoi je préfère cela, pour moi c'est plus clair.
Votre avis ?
Mon avis, c'est que la théorie des DL est "un poil" plus compliquée que les identités remarquables...
Cela dit, on comprend comme on le sent le mieux.
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 02 Sep 2008, 21:21
par le_fabien » 02 Sep 2008, 21:21
J'ai utilisé une notion de niveau lycée , moi je l'aime bien . :zen:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 02 Sep 2008, 21:25
par leon1789 » 02 Sep 2008, 21:25
Heu, le théorème des accroissements finis, et les DL , au lycée ? ok.... :hein: (en Belgique ?)
Et les identités remarquables ? :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités