Défilycée 6

par **baptisted** » 13 Juil 2008, 23:36

Et voici la nouvelle épreuve pour la 6eme édition du défilycée !! Alors je vous donne un exo qui m'a posé problème cette année... et que donc je vous ressert

:

Il suffit de montrer que

... +

est majorée par 2 autrement que par une simple récurrence.

càd :

Buena suerte !

par **sue** » 14 Juil 2008, 00:27

par **sue** » 14 Juil 2008, 00:36

Bonsoir,

baptisted a écrit:
càd : (pardonnez moi je ne sais pas pourquoi k=1 à n est à droite est pas en bas :mur: ... enfin vous aurez compris ^^

Buena suerte !

voilà :

si tu veux voir le code tu pointe le curseur sur l'expression

par **Zweig** » 14 Juil 2008, 00:49

Salut,

Remarquons que pour tout entier naturel

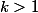
nous vons :

Ainsi,

par **baptisted** » 14 Juil 2008, 00:53

Zweig a écrit:Salut,

Remarquons que pour tout entier naturel nous avons :

Ainsi,

Eh bien mon défi n'a pas tenu longtemps :ptdr:!! Félicitation à toi Zweig, à toi de poser le septième défi !!

Et merci à Sue pour la formule !

par **Zweig** » 14 Juil 2008, 00:54

Faut que ce soit quoi comme type d'exercice ? Faut que ce soit résolvable pour des T°S uniquement ?

par **Ruch** » 14 Juil 2008, 00:55

Un peu rhétorique le défi...

par **baptisted** » 14 Juil 2008, 00:59

Ruch a écrit:Un peu rhétorique le défi...

Comment ça un peu rhétorique ?

par **Ruch** » 14 Juil 2008, 01:03

Ca rejoint la définition des questions rhétoriques, dont la réponse est déjà connu. Trivial si tu veux^^

par **baptisted** » 14 Juil 2008, 01:11

:ptdr:La prochaine fois, je donnerai quelque chose de hard...

Non plus sérieusement, penser à

c'est trivial pour quelqu'un qui ne l'a jamais vu ?

par **Zweig** » 14 Juil 2008, 01:14

C'est "trivial" pour ceux qui sont habitués aux "sommes télescopiques" :++:

Puisque la forme de tous les termes se ressemblent, il suffit d'étudier dans un premier temps 1/k². On veut 1/k² < ... et dans ce genre d'exo, faut essayer de 'décomposer" 1/k² de sorte d'arriver à une expression où les termes s'annulent les uns à la suite des autres. Après "tâtonnements", on arrive à cette expression

par **baptisted** » 14 Juil 2008, 01:25

Zweig a écrit:C'est "trivial" pour ceux qui sont habitués aux "sommes télescopiques" :++:

Puisque la forme de tous les termes se ressemblent, il suffit d'étudier dans un premier temps 1/k². On veut 1/k² < ... et dans ce genre d'exo, faut essayer de 'décomposer" 1/k² de sorte d'arriver à une expression où les termes s'annulent les uns à la suite des autres. Après "tâtonnements", on arrive à cette expression

Je suis d'accord, mais les sommes télescopique on n'en fait pas trop en Terminale en général. Personnellement on en a fait mais c'était dans le cadre d'un cours "vers la sup" sur les séries et les équivalents.

Défilycée 6

Défilycée 6

Qui est en ligne