Défilycée 5
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 11 Juil 2008, 19:55
par sue » 11 Juil 2008, 19:55
Salut

je ne suis plus au lycée , mais je propose de redonner vie à l'initiative de Yos , peut être il y aura plus d'interessés cette fois-ci

je relance le coup de départ par un exo sympa :
soientt
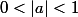
et
(1+a^2)...(1+a^{2^n}))
calculer la limite de
_n)
.
Bonne réflexion

ps: je rapelle juste le principe , qui proposera le premier une bonne réponse pourra lancer un autre défi et ainsi de suite .
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 11 Juil 2008, 20:34
par _-Gaara-_ » 11 Juil 2008, 20:34
Salut ^^
comme ça je dirais: 0 non ? (ou 1 mdrrrrr XD) :ptdr:
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 11 Juil 2008, 21:17
par sue » 11 Juil 2008, 21:17
comme ça je dirai : une preuve ? ;)
en tt cas , ni l'un ni l'autre :p
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 11 Juil 2008, 21:27
par _-Gaara-_ » 11 Juil 2008, 21:27
lol je savais ^^
je suis vraiment claqué sue
j'essayerais demain
=)

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 11 Juil 2008, 22:20
par raito123 » 11 Juil 2008, 22:20
Salut,
La suite est-elle définit :
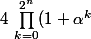)
ou bien
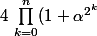)
??
Les multiples ne doivent pas être utilisés sans nécessité
-
samah
- Membre Relatif
- Messages: 257
- Enregistré le: 01 Juil 2008, 22:49
-
 par samah » 11 Juil 2008, 22:21
par samah » 11 Juil 2008, 22:21
raito123 a écrit:Salut,
La suite est-elle définit :
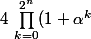)
ou bien
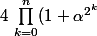)
??
je pense que c'est la même chose , non :hein:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Juil 2008, 22:27
par yos » 11 Juil 2008, 22:27
raito123 a écrit: 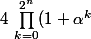)
ou bien
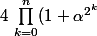)
??
Le second, sinon à quoi servirait de s'arrêter à l'exposant

?
-
samah
- Membre Relatif
- Messages: 257
- Enregistré le: 01 Juil 2008, 22:49
-
 par samah » 11 Juil 2008, 22:31
par samah » 11 Juil 2008, 22:31
yos a écrit:Le second, sinon à quoi servirait de s'arrêter à l'exposant

?
si c'était le cas , a quoi servirait de s'arreter à n , je pense que c'est bien pareil =D

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 11 Juil 2008, 22:37
par raito123 » 11 Juil 2008, 22:37
Non ça revient pas à la même chose !!
Les multiples ne doivent pas être utilisés sans nécessité
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Juil 2008, 22:38
par yos » 11 Juil 2008, 22:38
Raito demande si
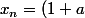(1+a^2)(1+a^3)(1+a^4)...(1+a^{2^n}))
(

facteurs),
ou bien
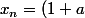(1+a^2)(1+a^4)...(1+a^{2^n}))
(n facteurs).
Aucune raison pour qu'on obtienne le même résultat.
Cependant je dis que la première possibilité est improbable sinon on aurait mis
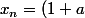(1+a^2)(1+a^3)(1+a^4)...(1+a^{n}))
qui donne bien le même résultat car
(1+a^2)(1+a^3)(1+a^4)...(1+a^{2^n}))
en est une suite extraite.
-
samah
- Membre Relatif
- Messages: 257
- Enregistré le: 01 Juil 2008, 22:49
-
 par samah » 11 Juil 2008, 22:40
par samah » 11 Juil 2008, 22:40
yos a écrit:Raito demande si
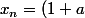(1+a^2)(1+a^3)(1+a^4)...(1+a^{2^n}))
(

facteurs),
ou bien
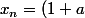(1+a^2)(1+a^4)...(1+a^{2^n}))
(n facteurs).
Aucune raison pour qu'on obtienne le même résultat.
Cependant je dis que la première possibilité est improbable sinon on aurait mis
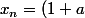(1+a^2)(1+a^3)(1+a^4)...(1+a^{n}))
qui donne bien le même résultat car
(1+a^2)(1+a^3)(1+a^4)...(1+a^{2^n}))
en est une suite extraite.
ah ok , je vois maintenat

-
baptisted
- Membre Naturel
- Messages: 48
- Enregistré le: 11 Juil 2008, 23:44
-
 par baptisted » 12 Juil 2008, 03:25
par baptisted » 12 Juil 2008, 03:25
Je ne crois pas me tromper en disant que cette limite est

...
Par contre faire la preuve en Latex sur le forum me fait peur surtout à 4h20 du matin... C'est pourquoi je me contente d'un .pdf réalisé avec Mathype + Word disponible
ici .
Cela me semble juste...
PS : Ca fait 2 jours que j'ai commencé Latex, ça va venir

.
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 12 Juil 2008, 09:13
par gol_di_grosso » 12 Juil 2008, 09:13
baptisted a écrit:Cela me semble juste...
Pour moi c'est bon.
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 12 Juil 2008, 09:31
par _-Gaara-_ » 12 Juil 2008, 09:31
Pas mal Baptiste :++:
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 12 Juil 2008, 17:35
par sue » 12 Juil 2008, 17:35
baptisted a écrit:Je ne crois pas me tromper en disant que cette limite est

...
Par contre faire la preuve en Latex sur le forum me fait peur surtout à 4h20 du matin... C'est pourquoi je me contente d'un .pdf réalisé avec Mathype + Word disponible
ici .
Cela me semble juste...
PS : Ca fait 2 jours que j'ai commencé Latex, ça va venir

.
Bravo Baptiste !
Je te passe le relais pour Défilycée 6

Sinon , on peut aussi exploiter une petite astuce qui donne immédiatement le résultat : multiplier

par (1-a)
c'est clair que
x_n=(1-a^{2^n}))

d'ou

-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 12 Juil 2008, 18:33
par _-Gaara-_ » 12 Juil 2008, 18:33
sue a écrit:Sinon , on peut aussi exploiter une petite astuce qui donne immédiatement le résultat : multiplier

par (1-a)
c'est clair que
x_n=(1-a^{2^n}))

d'ou

mdr !!! super l'astuce :doh: :doh: :doh:
-
baptisted
- Membre Naturel
- Messages: 48
- Enregistré le: 11 Juil 2008, 23:44
-
 par baptisted » 12 Juil 2008, 20:36
par baptisted » 12 Juil 2008, 20:36
Avec cette astuce j'ai l'impression d'avoir perdu mon temps avec ma preuve :briques: ... Mais je me met à chercher un défi... J'imagine que ça doit être niveau Terminale ? Ou peut-on dépasser un peu ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 12 Juil 2008, 20:41
par sue » 12 Juil 2008, 20:41
en fait, à l'origine c'est bien de Défilycée qu'il s'agit ...
ps: et tu peux ouvrir une autre discussion !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 13 Juil 2008, 10:12
par yos » 13 Juil 2008, 10:12
baptisted a écrit:Avec cette astuce j'ai l'impression d'avoir perdu mon temps avec ma preuve
Ta preuve et l'astuce, c'est deux fois la même chose. Tu as détaillé l'astuce simplement. En effet la réduction de proche en proche de
x_n)
nécessite une récurrence (ce que tu as fait). Sue a juste rendu le truc plus visuel.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
