Défilycée 1
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 02 Fév 2007, 13:12
Bonjour.
La rubrique supérieur accueille des défis depuis quelque temps. Le succès est au rendez-vous. Peut-être que les lycéens apprécieraient aussi. J'initie donc un cycle de défilycées par le problème suivant :
Soit ABC un triangle rectangle en A d'aire S. Son cercle inscrit touche le segment [BC] en un point K. Démontrer que
.
-
lysli
- Membre Rationnel
- Messages: 875
- Enregistré le: 16 Fév 2006, 00:07
-
par lysli » 02 Fév 2007, 14:06
Salut yos ,
j'ai une petite question :lol2:
Le triangle ABC est rectangle en quoi ?
:happy2:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 02 Fév 2007, 14:28
Rectangle en A!!! Je corrige illico.
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
par sue » 02 Fév 2007, 21:18
bonsoir ,
trés bonne initiative Yos :we:
je propose ceci :
le cercle inscrit touche [AB] , [AC] , [BC] resp. en I , J , K .
soient :
,
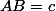
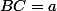
et
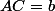
et on a :
et
et
selon les transformations de Ravi , on a :
et
.
donc :
-b)((a+b)-c)}{4} = \frac{a^2-(c^2+b^2)+2bc}{4} = \frac{a^2-a^2+2bc}{4}=\frac{bc}{2}=S)
cqfd .
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 03 Fév 2007, 00:16
Bravo sue!
Tu peux en poser aussi!
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
par sue » 03 Fév 2007, 09:52
bonjour,
ok , merci Yos . :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
