Courte question sur les suites...

par **Ladislas** » 07 Nov 2005, 19:14

Bonjour à tous,

Petite question qui me tarrode l'esprit sur les suites : Peut on determiner la formule d'une suite Un, à partir de Un+1 ?
Par exemple, je connais Un+1 = Un²-Un+1, et je veux trouver la formule Un, est-ce possible ?

Merci pour vos réponses !

Ladislas

par **Ladislas** » 07 Nov 2005, 19:35

Sachant que U0 = 2

par **Ladislas** » 07 Nov 2005, 20:59

Bon, en reisant, je trouve ce message bidon, je recommence avec l'énoncé :

Soit la suite Un définie par la formule Un+1 = Un²-Un+1 et par son premier terme U0 = 2.

Montrer par récurrence que pour tout n appartenant à N, Un >(ou égal) 2.

Voila, je vous remercie pour vos réponses en cette heure tardive !

Ladislas

par **Mikou** » 07 Nov 2005, 21:05

Bien sur ... ecris les 5 premiers termes de un que remarque tu ? ( utilise la recurrence pour demontrer l expression de Un que tu as conjecturé ... :we: )

par **Ladislas** » 07 Nov 2005, 21:13

Ok,
U1 = 3
U2 = 7
U3 = 43
U4 = 1807...
Je dois avouer que ces résultats ne m'inspirent guère...
Je n'arrive toujours pas à montrer que Un>(ou egale) 2.
Je l'ai fait avec Un+1, et ça me donne 3, esct ce que je dois partir de ce resultat ?
Merci pour vos réponses

par **Galt** » 07 Nov 2005, 21:29

Montrer par récurrence, c'est montrer de proche en proche.
Tu montres que si

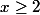
alors

ce qui est facile
Maintenant :

donc

c'est-à-dire

Puis

donc

c'est-à-dire

Puis

donc

c'est-à-dire

Etc...
Faire une récurrence, c'est écrire cet etc... de façon quelconque :
On suppose

donc

c'est-à-dire

Et voila, récurrence

par **Ladislas** » 07 Nov 2005, 21:58

Merci pour ta réponse claire, mais je n'ai pas bien saisi comment tu déduis que

à

directement

par **Ladislas** » 07 Nov 2005, 22:07

Voici comment j'ai procédé :

Supposons que

, vrai au rang

, alors

et comme nous savons que le premier terme

alors c'est vrau pour tout n appartenant à N !

ça doit etre ça non?
Merci pour vos réponses !

par **Galt** » 07 Nov 2005, 22:26

Ladislas a écrit:Merci pour ta réponse claire, mais je n'ai pas bien saisi comment tu déduis que à directement

Je prouve que si

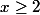
alors

par exemple en étudiant les variations de la fonction

par **Ladislas** » 07 Nov 2005, 22:31

:++: Ok, j'ai compris. Et penses tu que mon raisonnement un peu plus haut est correct ? J'hésite entreles deux en fait.
Merci pour vos réponses.

Courte question sur les suites...

Courte question sur les suites...

Qui est en ligne