Cos(x)-sin(x)=A

par **super_teufel** » 09 Déc 2006, 19:33

Salut tlm,

Ma question est simple... Il est-t-il possible d'isoler le x dans une équation du type cos(x)-sin(x)=A?

Merci d'avance!

par **rene38** » 10 Déc 2006, 01:52

Bonjour

en utilisant :

puis

par **euclide** » 11 Déc 2006, 09:44

En utilisant les nombres complexes j'ai trouvé ca :

x = Arccos

-

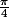
A noter que si |A|>

alors il n'y a pas de solutions et que les solutions données par cette formule ont valeurs dans [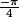

;

] mais que si x est une solution de l'équation dans cet interval alors

l'est aussi mais dans l'interval [

;

]. Donc quand |A|

il y a au moins une solution.

Pour arriver à ce résultat il faut utiliser le fait que :

cos(x) =

sin(x) =

par **fahr451** » 11 Déc 2006, 12:57

les complexes sont inutiles :
diviser les deux membres par racine de 2 et utiliser cos(x+pi/4)