Coordonnées de B et C.

par **Lagalère** » 04 Fév 2007, 15:21

Bonjour,j'ai quelques difficultés pour l'exercice suivant:

Dans un repère orthonormal(O;vect i,vect j),on donne le point A de coordonnées(3;4).
Sur la perpendiculaire en A à(OA),on prend les points B et C symétriques par rapport à A tels que le triangle BOC soit équilatéral.Le but de l'exercice est de trouver les coordonnées de B et C.
1/a)Calculer OA et démontrer que AB=5V3/3 (V pour racine carrée).
b)En déduire que,trouver les coordonnées de B et C,revient à trouver les vecteurs n de norme 5V3/3 orthogonaux à vect OA.
2/a)Trouver les vecteurs n.
b)En déduire que les droites(BH)et(AI)sont perpendiculaires.

Je vous remercie pour l'aide que vous voudriez bien m'apporter.

par **lexot** » 04 Fév 2007, 15:51

Bonjour

Si tu commençais ton exo, ce serait plus facile de t'aider

Cordialement

par **Lagalère** » 06 Fév 2007, 18:06

J'ai trouvé OA=5 mais,je ne sais pas,à partir de là,comment démontrer que

Lagalère a écrit:AB=5V3/3 (V pour racine carrée).

par **Lagalère** » 06 Fév 2007, 18:56

Vraiment personne ne peut m'aider?

par **Lagalère** » 06 Fév 2007, 19:48

Même un petit coup de pouce.

par **nyafai** » 06 Fév 2007, 20:08

bonjour
coup de pouce : il faut que tu utilises le fait que OAB est rectangle en A, que tu connais l'angle AOB (BOC est un triangle équilatéral...) et donc sa tangente et la valeur de OA.
bonne chance :we:

par **Lagalère** » 06 Fév 2007, 23:35

j'ai démontré que AB = 5V3 /3 mais comment en déduire que trouver les coordonnées de B et C revient à trouver les vecteurs n de norme 5V3/3 orthogonaux au vecteur OA et de trouver ces vecteurs n

par **Lagalère** » 07 Fév 2007, 16:18

Cette question-ci a été faite:

Lagalère a écrit:1/a)Calculer OA et démontrer que AB=5V3/3 (V pour racine carrée).

Mais,j'ai plus de difficultés à résoudre le reste du problème.

par **lexot** » 07 Fév 2007, 16:36

Bonjour

OA = 5
tan(AOB) = tan(30°) =

=

donc AB =

=

Soit B(x;y), donc

(x-3;y-4), et

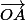
(3;4)
le produit scalaire

= 0 ; => 3x+4y-25 = 0 (1)

=

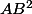
-6x -8y +25 =

(2)
(1) => y =

(3)

En remplaçant la valeur de y dans (2), on a :

-18x+11 = 0

x1 = 3 -

, et x2 = 3 +

y1 = 4 +

, et y2 = 4 -

Cordialement

par **Lagalère** » 18 Fév 2007, 00:05

Voilà,je comprends maintenant ce qu'il fallait faire.
Je vous remercie pour l'aide apportée et le temps passé.

Coordonnées de B et C.

Coordonnées de B et C.

Qui est en ligne