Cercles/Trigono
52 messages
- Page 1 sur 3 - 1, 2, 3
Cercles/Trigono
j'aimerais une piste svp... je cherche la solution à ces deux problèmes
"La section d´un cercle a un périmètre de 20cm. On demande l´angle au centre, la surface maximale de la section, et la mesure du rayon."
http://img329.imageshack.us/my.php?image=numro1nf8.png
__________________________________________________
"Nous avons deux rayons dans un cercle. Le point de rencontre entre les deux rayons, se nomment A et B. Nous relions A et B. Cela forme donc un triangle formé des deux rayons, et le segment reliant les deux points d´intersection. L´aire du triangle est de 1 cm carré. Son périmètre est de 4 cm. Quel est l´angle au centre, et la distance entre A et B?"
http://img329.imageshack.us/my.php?image=numro1nf8.png
"La section d´un cercle a un périmètre de 20cm. On demande l´angle au centre, la surface maximale de la section, et la mesure du rayon."
http://img329.imageshack.us/my.php?image=numro1nf8.png
__________________________________________________
"Nous avons deux rayons dans un cercle. Le point de rencontre entre les deux rayons, se nomment A et B. Nous relions A et B. Cela forme donc un triangle formé des deux rayons, et le segment reliant les deux points d´intersection. L´aire du triangle est de 1 cm carré. Son périmètre est de 4 cm. Quel est l´angle au centre, et la distance entre A et B?"
http://img329.imageshack.us/my.php?image=numro1nf8.png
slt,
dans le deuxieme probleme, le périmetre du cercle est il de 20 cm ?
si oui,
alors calculons le rayons du cercle :
2 * pi * R = 20 , R = 10/pi
2R + AB = 4 ; AB = 4 - 20/pi
Utilisons la formule de Al kashi (j'ai la flemme de la démontrer dsl) :
puis déduis en l'angle au centre que je note gamma. utilise la formule : P = gamma/360 * 2pi * R et tu auras la mesure de l'arc de cercle AB.
dans le deuxieme probleme, le périmetre du cercle est il de 20 cm ?
si oui,
alors calculons le rayons du cercle :
2 * pi * R = 20 , R = 10/pi
2R + AB = 4 ; AB = 4 - 20/pi
Utilisons la formule de Al kashi (j'ai la flemme de la démontrer dsl) :
puis déduis en l'angle au centre que je note gamma. utilise la formule : P = gamma/360 * 2pi * R et tu auras la mesure de l'arc de cercle AB.
Oh Désolé, je me suis gourrer.
Seulement dans le premier problème, le périmètre de la section est de 20 cm.
Pour le deuxième problème, nous savons seulement que le triangle isocèle n'est que de 1 cm carré, et a un périmètre de 4cm. Je me suis trompé de schéma.
Revoici les problèmes:
"La section d´un cercle a un périmètre de 20cm. On demande l´angle au centre, la surface maximale de la section, et la mesure du rayon."
http://img329.imageshack.us/my.php?image=numro1nf8.png
__________________________________________________
"Nous avons deux rayons dans un cercle. Le point de rencontre entre les deux rayons, se nomment A et B. Nous relions A et B. Cela forme donc un triangle formé des deux rayons, et le segment reliant les deux points d´intersection. L´aire du triangle est de 1 cm carré. Son périmètre est de 4 cm. Quel est l´angle au centre, et la distance entre A et B?"
http://img261.imageshack.us/my.php?image=numro2pe2.png
Seulement dans le premier problème, le périmètre de la section est de 20 cm.
Pour le deuxième problème, nous savons seulement que le triangle isocèle n'est que de 1 cm carré, et a un périmètre de 4cm. Je me suis trompé de schéma.
Revoici les problèmes:
"La section d´un cercle a un périmètre de 20cm. On demande l´angle au centre, la surface maximale de la section, et la mesure du rayon."
http://img329.imageshack.us/my.php?image=numro1nf8.png
__________________________________________________
"Nous avons deux rayons dans un cercle. Le point de rencontre entre les deux rayons, se nomment A et B. Nous relions A et B. Cela forme donc un triangle formé des deux rayons, et le segment reliant les deux points d´intersection. L´aire du triangle est de 1 cm carré. Son périmètre est de 4 cm. Quel est l´angle au centre, et la distance entre A et B?"
http://img261.imageshack.us/my.php?image=numro2pe2.png
EDIT : quel est le niveau de cet exercice ? si c'est au dessus de seconde il se peut qu'il y ai des formules trigonométriques que je n'ai pas bien retenu de mon bouquin de vacances de premiere.
Ok je me disais aussi...
exo 2 :
faisons un systeme de 2 équations :
AB + 2R = 4
Trouvons la deuxieme équation :
je calcule la hauteur avec pythagore, sachant que le triangle est isocele :
H² = R² - AB²/4
H = Racine(R² - AB²/4);
On a la hauteur
deuxieme équation :
(AB * H)/ 2 = 1
AB * H = 2
AB² * H² = 4
AB² * (R² - AB²) = 4
On a les deux équations a deux inconnues :
AB + 2R = 4 équivaut à : AB = 4 - 2R
AB²(R² - AB²) = 4 équivaut à : ((4 - 2R)R)² - (4 - 2 R)^4 = 4
bon bah apres bon courage pour la résolution, en tout cas moi je bloque un peu (j'ai pas exploiter toutes les possibilités, mais ca a l'air dur).
une fois AB trouvé, tu pourras utiliser al kashi pour trouver l'angle au centre (il y aura un cosinus dans l'équation), et puis apres avec cette angle tu pourras calculer l'arc de cercle Ab avec la formule que je t'ai donnée précédemment.
bye
Ok je me disais aussi...
exo 2 :
faisons un systeme de 2 équations :
AB + 2R = 4
Trouvons la deuxieme équation :
je calcule la hauteur avec pythagore, sachant que le triangle est isocele :
H² = R² - AB²/4
H = Racine(R² - AB²/4);
On a la hauteur
deuxieme équation :
(AB * H)/ 2 = 1
AB * H = 2
AB² * H² = 4
AB² * (R² - AB²) = 4
On a les deux équations a deux inconnues :
AB + 2R = 4 équivaut à : AB = 4 - 2R
AB²(R² - AB²) = 4 équivaut à : ((4 - 2R)R)² - (4 - 2 R)^4 = 4
bon bah apres bon courage pour la résolution, en tout cas moi je bloque un peu (j'ai pas exploiter toutes les possibilités, mais ca a l'air dur).
une fois AB trouvé, tu pourras utiliser al kashi pour trouver l'angle au centre (il y aura un cosinus dans l'équation), et puis apres avec cette angle tu pourras calculer l'arc de cercle Ab avec la formule que je t'ai donnée précédemment.
bye
lapras a écrit:Non,
(H * AB)/2 = 1 donc (H² * AB²)/4 = 1
donc H² * AB² = 4
j'ai 16 ans aussi, je pense que tu dois avoir a peu pres les memes connaissances que moi, mais dis moi, es tu censé apprendre des formules trigonométriques ? du genre sin(a + b) = ... ?
>Oui mais quand on voit H²= R² - AB²/4
On remplace le H² dans H² * AB² = 4 ce qui nous donne AB²(R² - AB²/4) = 4
Ta première équation serait AB²(R² - AB²/4) = 4 au lieu de AB²(R² - AB²) = 4
ouai okay
alors le système de lapras en gros c'était ça :
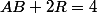

donc on en tire ce système :
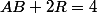
\time AB=AB\time R^2-\frac{AB^3}{4})
En remplaçant dans la 2e équation AB par son expression en fonction de R, on aR^2-\frac{(4-2R)^3}{4})
Donc tu développes...et tu obtiens cette équation du second degré de discriminant nul : 4R²-12R+9=0.
Et tu trouves R=4/3 et tu en déduis AB=4/3.
alors le système de lapras en gros c'était ça :
donc on en tire ce système :
En remplaçant dans la 2e équation AB par son expression en fonction de R, on a
Donc tu développes...et tu obtiens cette équation du second degré de discriminant nul : 4R²-12R+9=0.
Et tu trouves R=4/3 et tu en déduis AB=4/3.
52 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
