Arithmétique difficile
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 07 Oct 2007, 16:28
par J-R » 07 Oct 2007, 16:28
bonsoir,
autrement dit la somme de 2 des carrés consécutifs n'est jamais un cube parfait....
je n'ai trouvé aucune piste. :triste:
merci
a+
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 07 Oct 2007, 16:44
par J-R » 07 Oct 2007, 16:44
bien sur que ca m'intéresse
ca pourra me donner une piste de réflexion :)
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 07 Oct 2007, 16:55
par J-R » 07 Oct 2007, 16:55
j'avais pas pensé à la parité
mais ca à l'air de pas marcher dans l'autre sens
merci
je cherche encore.....
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 07 Oct 2007, 16:57
par lapras » 07 Oct 2007, 16:57
salut J-R !
Développe et trouve :
m² + (m+1)² = 2m(2m+1) + 1
impair quelque soit m
Donc si p existe il est necessairent impaire.
donc on pose :
p = 2k+1
(2k+1)^3 = 8k^3 + 12k² + 3k + 1 = k(8k²+12k+3) + 1
deux cas :
k impaire :
k = 2k' + 1
J'essaye de trouver une absurdité...
EDIT :
Si k impaire, alors
2m(2m+1) = (2k'+1)(2*(15k'²+28k') + 23)
ce qui est impaire
or 2m(2m+1) paire : k ne peut pas etre impaire
reste a prouver que k ne peut etre paire.
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 07 Oct 2007, 17:07
par J-R » 07 Oct 2007, 17:07
salut lapras:
pourquoi ce dévellopment de (2k+1)^3 ?
que sont u et v ?
merci d'avoir chercher ....
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 07 Oct 2007, 17:09
par lapras » 07 Oct 2007, 17:09
pardon, j'ai mis des u au lieu des k'
On a prouvé que si m²+(m+1)² était un cube, alors p était impaire
j'ai donc eu le reflexe de l'acrire 2k+1 et de développer au cube pour chercher une absurdité.
Apres l'absurdité ne vient pas directement, il faut décomposer a nouveau avec les parités :
On pose k impaire : c'est impossible
si on prouve que k paire impossible, alors on aura prouvé qu'un tel p n'existe pas
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 07 Oct 2007, 17:15
par J-R » 07 Oct 2007, 17:15
oui d'accord pour le raisonnment mais (2k+1)^3=8k^3+12k^2+6k+1
je regarde ce que je peux faire avec ca ....
merci
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 07 Oct 2007, 17:26
par lapras » 07 Oct 2007, 17:26
je viens de montrer que m ne peut etre impaire
donc m paire
je suis sur le point de trouver, je sens le truc venir
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 07 Oct 2007, 18:07
par aviateurpilot » 07 Oct 2007, 18:07
essaye de montrer que
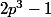
ne peux pas etre un carré parfait.
si tu montre ca alors
^2)
^2+m^2)
ou bien on utilisant le fait que
=(x+1)^2+x^2)
est stricte croissante sur

essaye de montrer que
<f(\frac{\sqrt{2p^2-1}-1}{2})<f(m+1))
ou
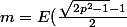)
donc
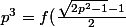\not\in f(\mathbb{N}))
resumé:
tt revien a montrer que
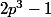
ne peux pas etre un carré parfait.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 07 Oct 2007, 19:53
par lapras » 07 Oct 2007, 19:53
Bonsoir !
Merci pour ton aide aviateurpilote !
Je n'aurais pas pensé à p^3 = f((sqrt(2p²-1) - 1)/2))
Sinon, pour montrer que 2p^3 - 1 n'est pas un carré parfait, sans utiliser ta fonction, comment on fait ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités