Anneaux

[Maxx1805]

Bonjour je me demandais si l'assertion suivante est vraie?
Soit un anneaux et E un ensemble quelconque, s'il existe un isomorphisme de l'anneaux dans E alors E est un anneaux

[Mimosa]

Bonjour

Tu ne peux pas parler d'isomorphisme qu'entre deux ensembles munis de la même structure; ta question telle que tu la poses n'a aucun sens.

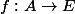En revanche, si tu disposes d'un anneau , d'un ensemble et d'une bijection , tu peux définir des lois sur en posant pour tout

.


Ce serait un bon exercice de prouver que ces lois font de un anneau isomorphe à

[LB2]

Sans supposer aucune structure sur E, tu peux également regarder l'ensemble des fonctions de E dans A et tenter de munir cet ensemble de fonctions d'une structure d'anneau... Quelles seraient les lois?

[Maxx1805]

Merci beaucoup
LB2 , l’anneau présenterait une loi d’addition (f+g)(x)=f(x)+g(x) et une loi multiplicative (fg)(x)=f(x)g(x) qui respecte les axiomes