Un anneau

[Dacu]

Bonsoir à tous,

Soit un anneau avec la propriété , .



Cordialement,

Dacu

[Dacu]

Bon matin à tous,

Certains disent que .Est-ce vrai?

Cordialement,

Dacu

[pascal16]

dans Z/2Z, c'est vrai.
mais Z/2Z est intègre, commutatif et contient assez peu d'éléments.

2018 ne se met pas directement sous une forme x²-3x, il faut réfléchir un peu.

par contre 2068 = 47²-3*47=0

[aviateur]

Bonjour
J'ai un peu regardé ta question hier mais vite et je pense avoir aussi trouvé aussi zéro mais je n'en suis pas sûr. Mais avant d'aller plus loin ton anneau est unitaire? commutatif? (ça cela doit jouer un rôle non?)

[Ben314]

Si A est unitaire, c'est vite plié : on a donc et il s'ensuit que, pour tout entier naturel pair N (donc par exemple N=2018) on a et donc pour tout .

[Dacu]

Bonjour à tous,

La solution proposée par certains:

De il en résulte ce qui signifie que et et .Ausi , de il en résulte ce qui signifie que et .En conclusion, il s'ensuit que .Le raisonnement est-il correct?

Cordialement,

Dacu

[Ben314]

Tu passe comment de 4x^2=0 à 2x=0 ?

[Dacu]

Tu passe comment de 4x^2=0 à 2x=0 ?

Salut,

Certains disent que de il en résulte ...

Cordialement,

Dacu

[Ben314]

Et tu en pense quoi toi d'un tel raisonnement ?

[pascal16]

dans Z/4Z : 2*2=0.
dis que 2 n'est pas régulier, mais on peut se passer du commutatif par contre

avec les matrices, si je dis pas de bêtise : (projecteur orthogonal selon une direction)*(projecteur selon son orthogonal)=0

[Dacu]

Et tu en pense quoi toi d'un tel raisonnement ?

Salut,

Je ne crois rien ...Je veux connaître la réponse à la question .Merci beaucoup!

Cordialement,

Dacu

[pascal16]

2018=46²+2
=3*46+2
= 140
= 11²+19
=33+19
=52
=7²+3
=24
=6²-12
=6
=4²-10
=2 (a priori irréductible)
=-2

2018x=2x

[Pseuda]

Bonjour,

@pascal16, attention tes entiers 46, etc... n'appartiennent pas à A. 46x , c'est juste x additionné à lui-même 46 fois.

Pour ma part, j'arrive au mieux à 6x=0, et 2x^2=0.
Cela fait 2018x=2x. Il y a peut-être mieux, et existe-t-il un tel anneau (à part isomorphe à Z/2Z) ?

[pascal16]

fo que je revois ma décomposition

[pascal16]

1 est dans A donc 3 est dans A et 1=3
3 est dans A donc 9 est dans A et rien 9= 9 n'apporte rien
9 est dans A donc 27 et 81 aussi et 27=81
27 est dans A donc 81 et 729 aussi et 729=81
81 est dans A donc 243 et 6561 aussi et 243=6561
243 est dans A donc 729 aussi et 729=59049
729 est dans A donc 2187 aussi et 2187 =531441

2187 =2018+81+81+3+3+1

2018=729 +729 + (81, 6fois) +27+27+9+9+1+1

2018= (27, 10fois) +9+9+1+1

2018= 27*(9+1) + 9 + 9+ 1+1

[Pseuda]

1 n'est pas forcément dans A, sinon c'est trivial (message de @Ben314 du 23/08 à 20h00).

On a aussi x^n = x^2 pour tout x dans A et tout n entier >=2.

[Ben314]

Il y a peut-être mieux, et existe-t-il un tel anneau (à part isomorphe à Z/2Z) ?

Si un anneau commutatif unitaire est tel que
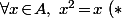Alors, du fait que on déduit que et on a donc comme le demande l'énoncé.
Après, les anneaux vérifiant (*), je sais pas si c'est pas ce qu'on appelle "les Anneaux de Boole" (à voir) et il y a non seulement Z/2Z, mais aussi (Z/2Z)^I où I est un ensemble quelconque qui est en fait isomorphe à l'ensemble P(I) des parties de I muni de la différence symétrique (=addition) et de l'intersection (=multiplication).

Et sauf erreur, il y a des anneaux autres que ceux là vérifiant (*) : Sur un anneau A vérifiant (*), on peut mettre une relation d'ordre définie par qui, dans le cas de P(I) correspond à la relation d'inclusion. Et pour que l'anneau A vérifiant (*)soit un P(I) (à isomorphisme prés bien sûr), il faut en particulier que pour cette relation d'ordre il y ait des éléments minimaux parmi les non nuls : dans le cas de P(I), ces éléments minimaux sont les singletons.

Mais bon, à part de monter qu'il existe un certain nombre d'anneaux vérifiant (*), ça ne répond pas vraiment à la question posée vu que ça me semble pas clair du tout que (*) est équivalent à (par contre (*) est évidement équivalent à )

Si jamais je continue à regarder la question, je pense que ce que je ferais, c'est de me remettre en mémoire les différentes construction d'anneaux, en particulier dans le cas le plus général (que je manipule rarement) non unitaire et non commutatif pour voir si on peut en construire un tel que mais pas .

Sinon, y'a aussi une méthode simple : c'est de considérer (comme c'est souvent le cas) que le terme "anneau" signifie "anneau unitaire" (c'est souvent le cas en Anglais où un anneau non unitaire est un pseudo-ring)

P.S. Parmi les A vérifiant (*) qui ne sont pas des P(I), il me semble bien qu'il y a, par exemple, l'ensemble des parties cofinies (i.e. de complémentaire fini) d'un ensemble (infini) X et d'autres trucs du même style comme les partie de [0,1] qui sont de mesure =1 : dans les deux cas, il n'y a pas d'élément minimaux pour la relation d'ordre.