je me suis demandé si le message d'erreur signifiait que
Python: tracer une fonction complexe.
6 messages
- Page 1 sur 1
Re: Python: tracer une fonction complexe.
Bonjour,
je me suis demandé si le message d'erreur signifiait que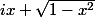 n'appartient pas au domaine de définition de ln(). Il faudrait qu'on sache comment est défini le log complexe en Python
n'appartient pas au domaine de définition de ln(). Il faudrait qu'on sache comment est défini le log complexe en Python
je me suis demandé si le message d'erreur signifiait que
Re: Python: tracer une fonction complexe.
quelques questions:
pourquoi le domaine de définition de la fonction (dont la courbe représentative est verte) inclut strictement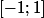 ?
?
pourquoi son image inclut strictement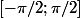 ?
?
ln désigne habituellement une fonction réelle . Par quelle demi-droite coupe-t-on le plan complexe pour définir le log complexe ? est-ce l'ensemble des réels négatifs ?
pourquoi le domaine de définition de la fonction (dont la courbe représentative est verte) inclut strictement
pourquoi son image inclut strictement
ln désigne habituellement une fonction réelle . Par quelle demi-droite coupe-t-on le plan complexe pour définir le log complexe ? est-ce l'ensemble des réels négatifs ?
Re: Python: tracer une fonction complexe.
On a
Z=e^{x+iy} =e^x e^{iy}
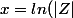 y=arg(Z)+k 2\pi) k étant un entier relatif quelconque
k étant un entier relatif quelconque
 =x+iy=ln(|Z|) +i (arg(Z)+k 2\pi))
Pour calculer log(Z), il faut définir une fonction
Arg() sur un ouvert simplement connexe du plan.
On peut prendre le plan complexe où l'on ôte la demi-droite
des réels négatifs ou nuls. On définit ainsi un domaine de définition du logarithme complexe.
Z=e^{x+iy} =e^x e^{iy}
Pour calculer log(Z), il faut définir une fonction
Arg() sur un ouvert simplement connexe du plan.
On peut prendre le plan complexe où l'on ôte la demi-droite
des réels négatifs ou nuls. On définit ainsi un domaine de définition du logarithme complexe.
Modifié en dernier par mathelot le 25 Mai 2021, 21:22, modifié 1 fois.
Re: Python: tracer une fonction complexe.
Bonjour, de ce que je peux voir de ton code, tu es en train de tracer le graphe de Im(z) en fonction de Re(z), et tu obtiens quelque chose qui a l'air correct : z est censé être réel (c'est l'arcsinus d'un réel entre -1 et 1) donc le graphe que tu demandes de tracer est un segment de droite horizontal. Les oscillations en 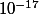 viennent sans doute d'erreurs d'arrondi/troncature.
viennent sans doute d'erreurs d'arrondi/troncature.
La courbe que tu veux c'est Re(z) en fonction de x.
La courbe que tu veux c'est Re(z) en fonction de x.
Re: Python: tracer une fonction complexe.
re,
log complexe
soient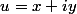 et
et  deux nombres complexes.
deux nombres complexes.
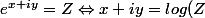)
Pour calculer log(Z), il faut donc déterminer x et y.
on a:
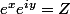 d'où
d'où 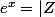 | d'où
| d'où 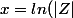) et il existe k dans
et il existe k dans  tel que
tel que 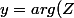+k 2 \pi)
d'où
= ln(|Z|)+i (arg(Z)+k 2 \pi))
La fonction log (logarithme complexe) est donc multivaluée. Pour un complexe Z donné non nul,
il y a une infinité de nombres complexes pour log(Z) (k peut prendre n'importe quelle valeur entière)
Pour définir une fonction log, on définit une fonction,) définie sur un ouvert simplement connexe du plan complexe. En général, on choisit comme ensemble de définition du log complexe le plan complexe privé de la demi-droite des réels négatifs ou nuls, et on pose Arg(1)=0.
définie sur un ouvert simplement connexe du plan complexe. En général, on choisit comme ensemble de définition du log complexe le plan complexe privé de la demi-droite des réels négatifs ou nuls, et on pose Arg(1)=0.
Pour l'arcsin
soit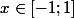 . Il existe
. Il existe  tel que
tel que 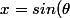) soit
soit 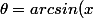)
On a donc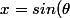) et
et 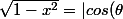|=cos(\theta).)
Donc .
.
Donc=ln(e^{i\theta})=ln(1)+i \theta=i \theta) et
et =\theta=arcsin(x))
log complexe
soient
Pour calculer log(Z), il faut donc déterminer x et y.
on a:
d'où
La fonction log (logarithme complexe) est donc multivaluée. Pour un complexe Z donné non nul,
il y a une infinité de nombres complexes pour log(Z) (k peut prendre n'importe quelle valeur entière)
Pour définir une fonction log, on définit une fonction
Pour l'arcsin
soit
On a donc
Donc
Donc
Re: Python: tracer une fonction complexe.
La courbe que tu cherchais à tracer est le graphe de la fonction réelle arcsin. Le fait que tu aies choisi d'écrire arcsin sous une forme qui fait intervenir des complexes ne change rien à l'affaire. Après tu peux tracer d'autres choses si tu veux, par exemple le segment de droite horizontal que tu traçais au début c'est l'image dans le plan complexe du segment [-1,1] par la fonction arcsin (c'est-à-dire le segment [-pi/2,pi/2]).
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
