Code correcteur

[Guitou80]

Bonjour,

Soit un code de dimension k et de longueur n

S'agit-il de l'application injective (On a k < n) B^k -> B^n (B étant l'ensemble booléen) ?

Si oui pourriez-vous svp m'expliquer pourquoi faut-il connaitre n*(2^k) bits pour définir le codage ?

Merci

[Rockleader]

Je ne sais pas trop quoi te dire aussi n'accorde pas beaucoup de crédit à ma réponse.

Toutefois j'aurais tendance à dire que le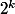 vient du fait que tu es en binaire, ça aurait un rapport avec la numération.

Pour le reste je ne comprends même pas les termes donc....désolé, mais je suis sur que certaines personnes seront capables de t'aider ici !

[didou31]

Bonjour,

Soit un code de dimension k et de longueur n

S'agit-il de l'application injective (On a k B^n (B étant l'ensemble booléen) ?

Si oui pourriez-vous svp m'expliquer pourquoi faut-il connaitre n*(2^k) bits pour définir le codage ?

Merci

C'est bien flou tout ça. Quelle est la longueur en bits des messages d'origine, de quelle fonction parle-t'on ? La fonction de correction ? La fonction de génération de code correcteur ?


Va voir du côté de la théorie des codes correcteurs de Hamming. C'est si je me souviens bien, la méthode optimale.