Bonjour,
Je me suis posé la question sur de combien de manières différentes pouvions-nous partitionner un entier n en somme d'entiers à commutativité près (par exemple, 5=5=4+1=3+2=3+1+1=2+2+1=2+1+1+1=1+1+1+1+1)
Pour ça j'ai calculé un algorithme récursif de ce type:
p(k, n)=p(k-1, n-1)+p(k-n, n) sauf si k ou n=1, 0,... (ici k représente l'entier à partitionner et n le nombre de termes de sa partition)
Y a-t-il moyen de simplifier cet algorithme à p(k)=? ? Si oui, comment?
Et encore mieux, y'aurait-t-il moyen de supprimer la récursivité et d'obtenir une simple formule? Ça serait génial!
Merci d'avance!
Algorithme récursif de partirions d'entiers
7 messages
- Page 1 sur 1
Re: Algorithme récursif de partirions d'entiers
Bonsoir,
Le théorème du nombre pentagonal d'Euler te permet de construire un un algorithme non récursif très simple.
Le théorème du nombre pentagonal d'Euler te permet de construire un un algorithme non récursif très simple.
Re: Algorithme récursif de partirions d'entiers
salut,
je doute qu'on puisse faire mieux (sinon on aurait déjà des résultats en ligne sur wikipedia) et si on peut faire mieux als c'est probablement pas efficient d'un point de vu calculatoire...
ya (normalement) deux raisons pour vouloir supprimer la récursivité:
1 - gagner en temps avec une autre méthode
2 - gagner en profondeur de recherche (à cause de la taille max de la stack)
pour 1) je vois pas (voir plus haut)
pour 2) tu peux toujours dérécursiver une fonction (moyennant plus ou moins d'efforts).
l'idée est très simple.
quand tu appeles une fonction avec k parametres.
le compilo met ces 4 paramètres dans une pile
il jump à la fonction.
il dépile ces 4 paramètres execute la fonction, ...
donc tt ce que tu a à faire c'est imiter ce comportement pour dérécursiver (d'un pnt de vue applicatif)
note: j'ai pas testé la validité des valeurs, j'ai juste choppé la formule chez wiki https://fr.wikipedia.org/wiki/Partition_d%27un_entier
je doute qu'on puisse faire mieux (sinon on aurait déjà des résultats en ligne sur wikipedia) et si on peut faire mieux als c'est probablement pas efficient d'un point de vu calculatoire...
ya (normalement) deux raisons pour vouloir supprimer la récursivité:
1 - gagner en temps avec une autre méthode
2 - gagner en profondeur de recherche (à cause de la taille max de la stack)
pour 1) je vois pas (voir plus haut)
pour 2) tu peux toujours dérécursiver une fonction (moyennant plus ou moins d'efforts).
l'idée est très simple.
quand tu appeles une fonction avec k parametres.
le compilo met ces 4 paramètres dans une pile
il jump à la fonction.
il dépile ces 4 paramètres execute la fonction, ...
donc tt ce que tu a à faire c'est imiter ce comportement pour dérécursiver (d'un pnt de vue applicatif)
- Code: Tout sélectionner
function p(n,k){
if(n<k||n==0||k==0){return 0}
if(n==k||n==1){return 1}
return p(n-1, k-1)+p(n-k,k)
}
function iterP(n,k){
var sum = 0;
var stack = [[n,k]];//p <k,n> values will be put here
while(stack.length){
let [n,k] = stack.pop();//as if we called the p
if(n<k||n==0||k==0){continue}
if(n==k||n==1){sum+=1; continue}
stack.push([n-1,k-1]);
stack.push([n-k,k]);
}
return sum;
}
note: j'ai pas testé la validité des valeurs, j'ai juste choppé la formule chez wiki https://fr.wikipedia.org/wiki/Partition_d%27un_entier
la vie est une fête 
Re: Algorithme récursif de partirions d'entiers
Salut,
Ce type de formule de récurrence mathématique, il faut absolument tout faire pour ne pas la taper telle quelle et sous forme récursive dans un ordi.
Je m'explique : on a par exemple p(100,18)=11 087 828 (11 millions)
(1) Si tu tape un algo. purement récursif, c'est on ne peut plus simple d'avoir une idée du nombre d'appel à la fonction récursive (1) : chaque appel final renvoie 0 ou 1 donc le nombre 11 087 828 a été obtenu uniquement en ajoutant des 0 et des 1 donc plus de dix million d'appel à la fonction (et a mon avis, c'est de l'ordre du double voire du triple : met un compteur avec une variable globale pour avoir une valeur exacte du nombre d'appel).
Et la raison de ce fait, elle est extrêmement simple : lors du calcul de p(100,18), la fonction p a été appelée un très très grand nombre de fois avec exactement les mêmes paramètre et à chaque fois, ben elle à refait absolument toute la descente récursive pour recalculer exactement le même résultat : c'est indubitablement totalement idiot comme méthode (tu peut de même rajouter dans la procédure un compteur ou tu mémorise dans une variable globale de type tableau le nombre de fois qu'elle a été appelée avec tel ou tel paramètre : la redondance est effarante)
(2) Alors que, si tu as suffisamment de place mémoire pour faire les calculs comme le ferait un tableur sous forme non récursive en calculant ligne par ligne les p(n,k) et en mémorisant les résultat alors tu as 1 calcul à faire sur la première ligne(n=1) ; 2 pour la deuxième; 3 pour la troisième; etc.. et pour remplir les lignes jusqu'à la 100em afin d'avoir p(100,18), ça te demande 1+2+3+...+100=5 050 calculs soit 2200 fois moins qu'avec la récursivité.
Et ça devient évidement de pire en pire lorsque n augmente vu que la méthode "tableur" est en O(n²) alors que je suis persuadé que la méthode récursive est de complexité exponentielle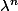 (par contre le
(par contre le  n'est pas complètement clair du fait de la référence à p(n-k,k))
n'est pas complètement clair du fait de la référence à p(n-k,k))
Après, évidement, LA question intéressante, c'est de savoir si on peut faire mieux que le temps totalement prohibitif de la méthode pure récursive sans bouffer des tonnes de mémoire à stocker tout le tableau.
Et là, effectivement, si ce qui t'intéresse c'est le nombre total p(n) de partition, je pense qu'il faut un peu faire des math pour écrire la formule différemment, par exemple, comme Al-Kashi le signale, tu as le théorème des nombres pentagonaux d'Euler.
(1) c.f. les fonctions p(n,k) "brute récursive"de fatal_error ci dessus.
EDIT : Après test, pour calculer p(100,18), la procédure de Fatal est appelée 197 333 761 fois (200 millions) mais il y a un bug dedans : il faut mettre "Si k==n ou k==1 alors . . ." et on passe à 25 651 079 appels (25 millions)
EDIT 2 : Vu la forme de la récursion, en plus sous la version "tableau", il te suffit d'avoir deux tableaux unidimensionnels correspondant à deux colonnes vu que le calcul de la k-ième colonne ne demande que la connaissance de la précédente. Et tu peut même t'en sortir avec un unique tableau unidimensionnel en grugeant un peu. Et bien évidement c'est nettement moins gourmand en place mémoire.
Perso, je suis de l'avis... totalement contraire....fatal_error a écrit:je doute qu'on puisse faire mieux (sinon on aurait déjà des résultats en ligne sur wikipedia) et si on peut faire mieux als c'est probablement pas efficient d'un point de vu calculatoire...
Ce type de formule de récurrence mathématique, il faut absolument tout faire pour ne pas la taper telle quelle et sous forme récursive dans un ordi.
Je m'explique : on a par exemple p(100,18)=11 087 828 (11 millions)
(1) Si tu tape un algo. purement récursif, c'est on ne peut plus simple d'avoir une idée du nombre d'appel à la fonction récursive (1) : chaque appel final renvoie 0 ou 1 donc le nombre 11 087 828 a été obtenu uniquement en ajoutant des 0 et des 1 donc plus de dix million d'appel à la fonction (et a mon avis, c'est de l'ordre du double voire du triple : met un compteur avec une variable globale pour avoir une valeur exacte du nombre d'appel).
Et la raison de ce fait, elle est extrêmement simple : lors du calcul de p(100,18), la fonction p a été appelée un très très grand nombre de fois avec exactement les mêmes paramètre et à chaque fois, ben elle à refait absolument toute la descente récursive pour recalculer exactement le même résultat : c'est indubitablement totalement idiot comme méthode (tu peut de même rajouter dans la procédure un compteur ou tu mémorise dans une variable globale de type tableau le nombre de fois qu'elle a été appelée avec tel ou tel paramètre : la redondance est effarante)
(2) Alors que, si tu as suffisamment de place mémoire pour faire les calculs comme le ferait un tableur sous forme non récursive en calculant ligne par ligne les p(n,k) et en mémorisant les résultat alors tu as 1 calcul à faire sur la première ligne(n=1) ; 2 pour la deuxième; 3 pour la troisième; etc.. et pour remplir les lignes jusqu'à la 100em afin d'avoir p(100,18), ça te demande 1+2+3+...+100=5 050 calculs soit 2200 fois moins qu'avec la récursivité.
Et ça devient évidement de pire en pire lorsque n augmente vu que la méthode "tableur" est en O(n²) alors que je suis persuadé que la méthode récursive est de complexité exponentielle
Après, évidement, LA question intéressante, c'est de savoir si on peut faire mieux que le temps totalement prohibitif de la méthode pure récursive sans bouffer des tonnes de mémoire à stocker tout le tableau.
Et là, effectivement, si ce qui t'intéresse c'est le nombre total p(n) de partition, je pense qu'il faut un peu faire des math pour écrire la formule différemment, par exemple, comme Al-Kashi le signale, tu as le théorème des nombres pentagonaux d'Euler.
(1) c.f. les fonctions p(n,k) "brute récursive"de fatal_error ci dessus.
EDIT : Après test, pour calculer p(100,18), la procédure de Fatal est appelée 197 333 761 fois (200 millions) mais il y a un bug dedans : il faut mettre "Si k==n ou k==1 alors . . ." et on passe à 25 651 079 appels (25 millions)
EDIT 2 : Vu la forme de la récursion, en plus sous la version "tableau", il te suffit d'avoir deux tableaux unidimensionnels correspondant à deux colonnes vu que le calcul de la k-ième colonne ne demande que la connaissance de la précédente. Et tu peut même t'en sortir avec un unique tableau unidimensionnel en grugeant un peu. Et bien évidement c'est nettement moins gourmand en place mémoire.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Algorithme récursif de partirions d'entiers
- Code: Tout sélectionner
#include <stdio.h>
#include <stdlib.h>
long int NbAdd;
long int p1(int n, int k)
{ if((n<k)||(n==0)||(k==0)){ return 0; }
if((n==k)||(k==1)){ return 1; }
NbAdd++;
return p1(n-1,k-1)+p1(n-k,k);
}
long int p2(int n, int k)
{ long int *Tb,ret; int m,i,j,jmax;
if((k<1)||(k>n)) return 0;
m=n-k; Tb=malloc((m+1)*sizeof(long));
for(i=0;i<=m;i++) Tb[i]=1;
jmax=(k<m)?k:m;
for(j=2;j<=jmax;j++) for(i=j;i<=m;i++) { Tb[i]+=Tb[i-j]; NbAdd++;}
ret=Tb[m]; free(Tb);
return ret;
}
int main(void)
{ int n,k;
n=130; k=21;
NbAdd=0; printf("p1(%d,%d)=%ld",n,k,p1(n,k)); printf(" ; NbAdd=%ld\n",NbAdd);
NbAdd=0; printf("p2(%d,%d)=%ld",n,k,p2(n,k)); printf(" ; NbAdd=%ld\n",NbAdd);
}
p1(130,21)=270 625 918 ; NbAdd=306 569 547
p2(130,21)=270 625 918 ; NbAdd=1 970
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Algorithme récursif de partirions d'entiers
juste pour info, dans le lien que j'ai donné, l'algo par récurrence est quadratique (par mémoisation) et juste en dessous, y est stipulé (je n'ai pas vérifié) une méthode plus efficace (celle dont vous parlez) à base des nombre penthagonaux d'euler (page que je n'ai _pas pris_ le temps de lire)
je suis ok avec toi, dans le sens qu'il y a souvent une méthode plus performante qu'une méthode récursive. (j'omets la mémoisation, parce que ca n'apporte "rien" d'un point de vue intellectuel, mettre un cache, bon...). Maintenant __je ne dis pas (et n'ai pas dit)__ qu'il faut tjs préférer une formule récursive... (du moins pour la complexité mémoire/et ou temporelle).
Je pourrais le dire d'un pt de vue logiciel lecture etc, mais ici on s'en fout.
je suis ok avec toi, dans le sens qu'il y a souvent une méthode plus performante qu'une méthode récursive. (j'omets la mémoisation, parce que ca n'apporte "rien" d'un point de vue intellectuel, mettre un cache, bon...). Maintenant __je ne dis pas (et n'ai pas dit)__ qu'il faut tjs préférer une formule récursive... (du moins pour la complexité mémoire/et ou temporelle).
Je pourrais le dire d'un pt de vue logiciel lecture etc, mais ici on s'en fout.
la vie est une fête 
Re: Algorithme récursif de partirions d'entiers
fatal_error a écrit:(j'omets la mémoisation, parce que ca n'apporte "rien" d'un point de vue intellectuel, mettre un cache, bon...)...
Je me doute bien que toi (et les autres que je connais qui font de l'info.) sont au courant de ce truc concernant récursivité/mémoïsation qui effectivement "n'apporte rien d'un point de vue intellectuel", mais qui permet d'améliorer de façon astronomique la complexité temporelle de la fonction (passage d'une complexité exponentielle à une complexité polynomiale dans le cas présent)
Mais par contre Maths314 c'est sa première intervention, et vu son (unique) laïus, j'étais pas du tout certain qu'il était conscient du phénomène donc je me suis fendu d'un exemple pour lui montrer la catastrophe que c'est (et ça pourra me resservir dans les T.D. d'algo. pour remplacer le sempiternel calcul des coefficients binomiaux par la même méthode "bêtement récursive"...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
