Bonjour,
Je bute sur un type de problème que je pourrais présenter d'une manière simplifiée de la manière suivante.
Soit un ensemble de 35 combinaisons à partir des numéros 1 à 7 pris 3 par 3.
Soit en développant les combinaisons suivantes
123 124 125 126 127 134 135 136 137 145 146 147 156 157 167
234 235 236 237 245 246 247 256 257 267
345 346 347 356 357 367
456 457 467
567
Existe t-il une formule mathématique permettant de trouver les éléments d'une combinaison en ayant que le numéro de la combinaison?
Par exemple
la combinaison 15 est composée des éléments 1, 6 et 7, celle portant le numéro 29 a pour éléments 3, 5 et 6.
Je vous remercie pour vos réponses.
Trouver les éléments d'une combinaison
7 messages
- Page 1 sur 1
Re: Trouver les éléments d'une combinaison
Salut,
Tout dépend de ce que tu appelle une "formule mathématique", mais par exemple au niveau informatique, oui, il y a un (voire plusieurs...) algorithmes simples.
On peut regarder sur un exemple en partant de ton truc avec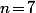 et
et 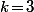 .
.
On part du triangle de pascal (contenant les coeff. binomiaux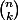 ) qui est facile à obtenir vu que le contenu d'une case est la somme de celle au dessus et de celle au dessus à gauche :
) qui est facile à obtenir vu que le contenu d'une case est la somme de celle au dessus et de celle au dessus à gauche :

On constate qu'effectivement, il y a 35 combinaisons de 3 éléments choisi parmi 7 et pour trouver par exemple quelle est la 8em combinaison on procède de la façon suivante :
 On calcule 35 - 8 = 27 et on cherche le nombre le plus bas de la colonne n=3 qui soit inférieur ou égal à 27.
On calcule 35 - 8 = 27 et on cherche le nombre le plus bas de la colonne n=3 qui soit inférieur ou égal à 27.
C'est 20 qui est sur la ligne k=6 : le premier nombre est 7 - 6 = 1.
 On calcule 27 - 20 = 7 et on cherche le nombre le plus bas de la colonne n=2 qui soit inférieur ou égal à 7.
On calcule 27 - 20 = 7 et on cherche le nombre le plus bas de la colonne n=2 qui soit inférieur ou égal à 7.
C'est 6 qui est sur la ligne k=4 : le deuxième nombre est 7 - 4 = 3.
 On calcule 7 - 6 = 1 et on cherche le nombre le plus bas de la colonne n=1 qui soit inférieur ou égal à 1.
On calcule 7 - 6 = 1 et on cherche le nombre le plus bas de la colonne n=1 qui soit inférieur ou égal à 1.
C'est 1 qui est sur la ligne k=1 : le troisième nombre est 7 - 1 = 6.
BILAN : la 8em combinaison est 136.
Pour la 15 em, combinaison, ça donnerais ça :
 35 - 15 = 20. Le plus bas de la colonne n=3 qui soit
35 - 15 = 20. Le plus bas de la colonne n=3 qui soit 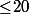 est 20 avec k=6 : le premier nombre est 7 - 6 =1.
est 20 avec k=6 : le premier nombre est 7 - 6 =1.
 20 - 20 = 0. Le plus bas de la colonne n=2 qui soit
20 - 20 = 0. Le plus bas de la colonne n=2 qui soit 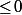 est 0 avec k=1 : le deuxième nombre est 7 - 1 =6.
est 0 avec k=1 : le deuxième nombre est 7 - 1 =6.
 0 - 0 = 0. Le plus bas de la colonne n=1 qui soit
0 - 0 = 0. Le plus bas de la colonne n=1 qui soit 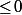 est 0 avec k=0 : le troisième nombre est 7 - 0 =7.
est 0 avec k=0 : le troisième nombre est 7 - 0 =7.
Et pour la 29 em, combinaison, ça donnerais ça :
 35 - 29 = 6. Le plus bas de la colonne n=3 qui soit
35 - 29 = 6. Le plus bas de la colonne n=3 qui soit 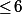 est 4 avec k=4 : le premier nombre est 7 - 4 =3.
est 4 avec k=4 : le premier nombre est 7 - 4 =3.
 6 - 4 = 2. Le plus bas de la colonne n=2 qui soit
6 - 4 = 2. Le plus bas de la colonne n=2 qui soit 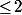 est 1 avec k=2 : le deuxième nombre est 7 - 2 =5.
est 1 avec k=2 : le deuxième nombre est 7 - 2 =5.
 2 - 1 = 1. Le plus bas de la colonne n=1 qui soit
2 - 1 = 1. Le plus bas de la colonne n=1 qui soit 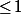 est 1 avec k=1 : le troisième nombre est 7 - 1 =6.
est 1 avec k=1 : le troisième nombre est 7 - 1 =6.
Tout dépend de ce que tu appelle une "formule mathématique", mais par exemple au niveau informatique, oui, il y a un (voire plusieurs...) algorithmes simples.
On peut regarder sur un exemple en partant de ton truc avec
On part du triangle de pascal (contenant les coeff. binomiaux
On constate qu'effectivement, il y a 35 combinaisons de 3 éléments choisi parmi 7 et pour trouver par exemple quelle est la 8em combinaison on procède de la façon suivante :
C'est 20 qui est sur la ligne k=6 : le premier nombre est 7 - 6 = 1.
C'est 6 qui est sur la ligne k=4 : le deuxième nombre est 7 - 4 = 3.
C'est 1 qui est sur la ligne k=1 : le troisième nombre est 7 - 1 = 6.
BILAN : la 8em combinaison est 136.
Pour la 15 em, combinaison, ça donnerais ça :
Et pour la 29 em, combinaison, ça donnerais ça :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trouver les éléments d'une combinaison
Salut,
Merci pour ta réponse. Elle convient pour l'exemple que j'ai proposé. Je comprends le recours au triangle de Pascal. Cela suppose de définir un tableau avec toutes les valeurs possibles au préalable.
Toutefois quand les ensembles deviennent importants du genre trouver les éléments de la combinaison 3021 parmi celles constituées dans l'ensemble des 4950 combinaisons à partir des numéros 1 à 100 pris 2 à 2.
ou pire si on considère l'ensemble des combinaisons au quinté ou au loto.
Je recherche une solution plus adaptée à des ensembles importants.
Merci pour ta réponse. Elle convient pour l'exemple que j'ai proposé. Je comprends le recours au triangle de Pascal. Cela suppose de définir un tableau avec toutes les valeurs possibles au préalable.
Toutefois quand les ensembles deviennent importants du genre trouver les éléments de la combinaison 3021 parmi celles constituées dans l'ensemble des 4950 combinaisons à partir des numéros 1 à 100 pris 2 à 2.
ou pire si on considère l'ensemble des combinaisons au quinté ou au loto.
Je recherche une solution plus adaptée à des ensembles importants.
Re: Trouver les éléments d'une combinaison
Ben non, tu est pas obligé de faire le tableau complet : il te suffit de faire une procédure qui prend comme paramètres deux entiers n et k et qui renvoie le coeff. binomial correspondant. Ca sera évidement plus long que s'ils sont déjà calculés dans un tableau, mais ça va quand même être très rapide.
Surtout qu'on peut (voire même on doit...) chercher la position d'un entier donné dans une colonne donnée du triangle de Pascal en procédant par dichotomie.
Le seul problème que tu risque de rencontrer avec certains langage, c'est un dépassement de capacité sur les entiers.
Surtout qu'on peut (voire même on doit...) chercher la position d'un entier donné dans une colonne donnée du triangle de Pascal en procédant par dichotomie.
Le seul problème que tu risque de rencontrer avec certains langage, c'est un dépassement de capacité sur les entiers.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trouver les éléments d'une combinaison
D'accord et quelle tête aurait cette procédure qui renvoie le coefficient binomial?
Re: Trouver les éléments d'une combinaison
Entrée : n et k (entiers)
Coeff = 1 ;
Pour i de 1 à k faire Coeff=Coeff*(n+1-i)/i
Sortie : Coeff
Coeff = 1 ;
Pour i de 1 à k faire Coeff=Coeff*(n+1-i)/i
Sortie : Coeff
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trouver les éléments d'une combinaison
Merci pour les réponses que tu m'as apportées.
Bonne journée
Bonne journée
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
