1=2 ?

par **Anonyme** » 16 Jan 2006, 21:43

a=b
a²=ab
a²-b²=ab-b²
(a-b)(a+b)=b(a-b)
a+b=b or a=b
2b=b
2=1

le théoreme du cancre ou comment faire dresser les cheveux sur la tete d'un prof de math

par **Alpha** » 16 Jan 2006, 21:47

shindara a écrit:(a-b)(a+b)=b(a-b)
a+b=b or a=b

Bonsoir, il s'agit en effet de l'arnaque archi-classique basée sur une division par 0 censée passer inaperçue... :ptdr:

Alpha+

par **Chimerade** » 17 Jan 2006, 00:29

Alpha a écrit:Bonsoir, il s'agit en effet de l'arnaque archi-classique basée sur une division par 0 censée passer inaperçue... :ptdr:

Alpha+

En effet, elle est plus vieille que moi, c'est dire...

par **Mikou** » 17 Jan 2006, 13:55

lol chimerade !

par **Alpha** » 17 Jan 2006, 17:03

Chimerade a écrit:En effet, elle est plus vieille que moi, c'est dire...

Bien vu, Papy! :ptdr:

par **yos** » 18 Jan 2006, 15:01

shindara a écrit:a+b=b or a=b
2b=b

Je ne vois pas le passage ci-dessus.

par **alecs20** » 18 Jan 2006, 15:46

Salut,

, mais a=b, alors

J'suis sur c'est juste une erreur d'inatention, en voyant tes posts, tu es très capable de faire ca yos.

C'est peut-être aussi parce que shindara a oublié de mentionner dans la preuve au départ que a=b=1.

par **yos** » 18 Jan 2006, 17:38

Désolé je ne suis pas tout.

Selon ce que tu dis, c'est le or qui devient mais qui est l'arnaque!?
Si oui, il n'y a pas lieu de supposer a=b=1 mais seulement

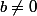
pour la dernière simplification.

Bon c'est un détail. Merci de m'avoir répondu.

par **alecs20** » 18 Jan 2006, 17:49

Resalut,

non l'arnaque est lorsqu'on simplifie les (a-b) a la 4e ligne, parce que ca fait 0/0 qui est une forme indeterminée.

par **yos** » 18 Jan 2006, 18:13

Non car l'alternative "a+b=b ou a=b" écrite par shindara est tout à fait correcte à partir de la ligne précédente "(a-b)(a+b)=b(a-b)".
Regarde bien la formulation.

par **alecs20** » 18 Jan 2006, 18:46

La formulation algebrique est correcte, mais pas numériquement puisque (a-b) = (1-1) = 0. Tout ce qui suit apres "(a-b)(a+b)=b(a-b)" est faux. On ne peut pas simplifier les (a-b).

par **Chimerade** » 18 Jan 2006, 18:51

yos a écrit:Non car l'alternative "a+b=b ou a=b" écrite par shindara est tout à fait correcte à partir de la ligne précédente "(a-b)(a+b)=b(a-b)".
Regarde bien la formulation.

Justement, shindara n'a pas écrit "a+b=b ou a=b" mais ceci :

[INDENT](a-b)(a+b)=b(a-b)
a+b=b or a=b[/INDENT]

Moi aussi, j'avais cru à une faute de frappe. Il manquait simplement un point :

a+b=b. Or, a=b, donc...
Il conclut donc définitivement que a+b=b - sans alternative à ce diktat - et c'est là que se situe l'arnaque. Puis il poursuit sa démonstration en s'appuyant sur a=b...

par **alecs20** » 18 Jan 2006, 18:58

Ahhh ok! Subtile est l'interprétation parfois.

par **alecs20** » 18 Jan 2006, 18:59

Ahhh ok! Subtile est l'interprétation parfois.

par **yos** » 18 Jan 2006, 19:03

Ah d'accord! Je me demandais pourquoi il mettait le "ou" en anglais. Il faut dire qu'on en voit de toute sorte dans les formulations alors voilà j'ai mal interprété le truc. Heureusement que Chim...erade était là.

par **alecs20** » 18 Jan 2006, 19:05

Haha yos, j'pense qu'il apprécit vraiment pas ton abbréviation avec son nickname!

1=2 ?

1=2 ?

Qui est en ligne